
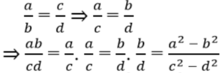
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

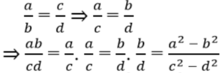

Có \(\frac{a}{b}=\frac{c}{d}\Leftrightarrow\frac{a^2}{b^2}=\frac{c^2}{d^2}=\frac{ac}{bd}\)
Mà \(\frac{a^2}{b^2}=\frac{c^2}{d^2}=\frac{a^2+c^2}{b^2+d^2}\)
Nên \(\frac{ac}{bd}=\frac{a^2+c^2}{b^2+d^2}\left(đpcm\right)\)
1. a) Đặt \(\frac{a}{b}=\frac{c}{d}=k\)
=> \(\hept{\begin{cases}a=bk\\c=dk\end{cases}}\)
Khi đó \(\frac{a}{3a+b}=\frac{bk}{3bk+b}=\frac{bk}{b\left(3k+1\right)}=\frac{k}{3k+1}\left(1\right)\)
\(\frac{c}{3c+d}=\frac{dk}{3dk+d}=\frac{dk}{d\left(3k+1\right)}=\frac{k}{3k+1}\left(2\right)\)
Từ (1) và (2) => \(\frac{a}{3a+b}=\frac{c}{3c+d}\)
c,
Đặt \(\frac{a}{b}=\frac{c}{d}=k\)
=> \(\hept{\begin{cases}a=bk\\c=dk\end{cases}}\)
Khi đó \(\frac{ab}{cd}=\frac{b^2k}{d^2k}=\frac{b^2}{d^2}\) (3)
\(\frac{a^2-b^2}{c^2-d^2}=\frac{\left(bk\right)^2-b^2}{\left(dk\right)^2-d^2}=\frac{b^2k^2-b^2}{d^2k^2-d^2}=\frac{b^2\left(k^2-1\right)}{d^2\left(k^2-1\right)}=\frac{b^2}{d^2}\left(4\right)\)
Từ (3) và (4) \(\Rightarrow\frac{ab}{cd}=\frac{a^2-b^2}{c^2-d^2}\)
@@ Học tốt
Chiyuki Fujito

ta có:
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a^6}{b^6}=\dfrac{c^6}{d^6}=\dfrac{3a^6}{3b^6}\)
Áp dụng tính chất dãy tỉ sốbằng nhau ta có:
\(\dfrac{a^6}{b^6}=\dfrac{c^6}{d^6}=\dfrac{3a^6}{3b^6}=\dfrac{a^6+c^6}{b^6+d^6}=\dfrac{\left(a+c\right)^6}{\left(b+d\right)^6}\)
=\(\dfrac{c^6+3a^6}{d^6+3b^6}\)
\(\Rightarrow\dfrac{3a^6+c^6}{3b^6+d^6}=\dfrac{\left(a+c\right)^6}{\left(b+d\right)^6}\) (ĐPCM)

Đặt \(\frac{a}{b}=\frac{c}{d}=k\)
\(\Rightarrow\)a=bk , c=dk
Ta có:
\(\left(\frac{a+b}{c+d}\right)^2=\frac{\left(a+b\right)^2}{\left(c+d\right)^2}=\frac{\left(bk+b\right)^2}{\left(dk+d\right)^2}=\)\(\frac{\left(b\left(k+1\right)\right)^2}{\left(d\left(k+1\right)\right)^2}=\frac{b^2\times\left(k+1\right)^2}{d^2\times\left(k+1\right)^2}=\frac{b^2}{d^2}\)( 1 )
\(\frac{a^2+b^2}{c^2+d^2}=\frac{\left(bk\right)^2+b^2}{\left(dk\right)^2+d^2}=\frac{b^2\times k^2+b^2}{d^2\times k^2+d^2}\)= \(\frac{b^2\times\left(k^2+1\right)}{d^2\times\left(k^2+1\right)}=\frac{b^2}{d^2}\)( 2 )
Từ ( 1 ) và ( 2 ) \(\Rightarrow\left(\frac{a+b}{c+d}\right)^2=\frac{a^2+b^2}{c^2+d^2}\)(dpcm)
* Giả sử tất cả các tỷ lệ thức đều có nghĩa.
\(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}\Rightarrow\frac{a}{c}\times\frac{b}{d}=\frac{b}{d}\times\frac{b}{d}\Rightarrow\frac{ab}{cd}=\frac{b^2}{d^2}=\frac{a^2}{c^2}=\frac{2ab}{2cd}\)
\(=\frac{a^2+2ab+b^2}{c^2+2cd+d^2}=\frac{\left(a+b\right)^2}{\left(c+d\right)^2}=\frac{a^2+b^2}{c^2+d^2}\)(ĐPCM)

ta có:
b^2=ac =>a/b=b/c (1)
c^2=bd =>b/c=c/d (2)
(1)(2)=>a/b=b/c=c/d
=>a^3/b^3=b^3/c^3=c^3/d^3=abc/bcd
=>(a^3+b^3+c^30)/(b^3+c^3+d^3)=a/d
Vay.......
Nhớ tick mk nha
ta có:
b^2=ac =>a/b=b/c (1)
c^2=bd =>b/c=c/d (2)
(1)(2)=>a/b=b/c=c/d
=>a^3/b^3=b^3/c^3=c^3/d^3=abc/bcd
=>(a^3+b^3+c^3)/(b^3+c^3+d^3)=a/d
Vay dpcm

cho hỏi chút
\(\frac{a}{b}=\frac{c}{d}\)
trong đó
\(a=c\) hay \(a\ne c\)
\(b=d\) hay \(b\ne d\)
( bài có thiếu điều kiện ko vậy )

Gọi \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=kb;c=kd\)(1)
Thay (1) vào ta có :
\(\frac{3a^2+c^2}{3b^2+d^2}=\frac{3\left(kb\right)^2+\left(kd\right)^2}{3b^2+d^2}=\frac{3k^2b^2+k^2+d^2}{3b^2+d^2}=\frac{k^2\left(3b^2+d^2\right)}{3b^2+d^2}=k^2\)(1)
\(\frac{\left(a+c\right)^2}{\left(b+d\right)^2}=\frac{\left(kb+kd\right)^2}{\left(b+d\right)^2}=\frac{\left[k\left(b+d\right)\right]^2}{\left(b+d\right)^2}=\frac{k^2.\left(b+d\right)^2}{\left(b+d\right)^2}=k^2\)(2)
Từ (1) và (2)
\(\Rightarrow\frac{3a^2+c^2}{3b^2+d^2}=\frac{\left(a+c\right)^2}{\left(b+d\right)^2}\)
\(\RightarrowĐPCM\)

Bài làm :
Ta có : \(b^2=ca\Rightarrow\frac{a}{b}=\frac{b}{c}\), \(c^2=bd\Rightarrow\frac{b}{c}=\frac{c}{d}\)
\(\Rightarrow\frac{a}{b}=\frac{b}{c}=\frac{c}{d}\Rightarrow\frac{a^3}{b^3}=\frac{b^3}{c^3}=\frac{c^3}{d^3}=\frac{a^3+b^3+c^3}{b^3+c^3+d^3}\) ( Tính chất dãy tỉ số bằng nhau ) (1)
Lại có : \(\frac{a^3}{b^3}=\frac{a}{b}.\frac{a}{b}.\frac{a}{b}=\frac{a}{b}.\frac{b}{c}.\frac{c}{d}=\frac{a.b.c}{b.c.d}=\frac{a}{d}\)
( Do \(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}\) ) (2)
Từ (1) và (2) \(\Rightarrow\frac{a^3+b^3+c^3}{b^3+c^3+d^3}=\frac{a}{d}\) ( đpcm )
Chúc bạn học tốt !!