Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có:
\(4a^2+b^2=5ab\Leftrightarrow4a^2+b^2-4ab-ab=0\)
\(\Leftrightarrow4a\left(a-b\right)-b\left(a-b\right)=0\)
\(\Leftrightarrow\left(a-b\right)\left(4a-b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a-b=0\\4a-b=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=b\left(ktm\right)\\4a=b\left(tm\right)\end{matrix}\right.\)
\(\Rightarrow4a=b\)
\(\Rightarrow\dfrac{5ab}{3a^2+2b^2}=\dfrac{5a.4a}{3a^2+2.\left(4a\right)^2}=\dfrac{20a^2}{3a^2+32a^2}\)
\(=\dfrac{20a^2}{35a^2}=\dfrac{4}{7}\)
\(4a^2+b^2=5ab\)
\(\Rightarrow4a\left(a-b\right)-b\left(a-b\right)=0\)
\(\Rightarrow\left(a-b\right)\left(4a-b\right)=0\)
\(\Rightarrow b=4a\left(do.a\ne b\right)\)
\(\dfrac{5ab}{3a^2+2b^2}=\dfrac{20a^2}{3a^2+32a^2}=\dfrac{4}{7}\)
\(Từ\) \(giả\) \(thiết\) : \(4a^2+b^2=\text{5}ab\)
\(\Leftrightarrow4a^2-4ab-ab+b^2\)
\(\Leftrightarrow\left(4a-b\right)\left(a-b\right)=0\)
\(TH1:\) \(4a-b=0\) \((\) \(mẫu\) \(thuẫn\) \(với\) \(2a>b\) \()\)
\(TH2:\) \(a-b=0\)
\(\Rightarrow a=b\)
\(\Rightarrow A=\dfrac{a^2}{4a^2-a^2}\)
\(\Rightarrow A=\dfrac{1}{3}\)
=>4a^2-5ab+b^2=0
=>(a-b)(4a-b)=0
=>a=b hoặc b=4a(loại)
=>P=b^2/3b^2=1/3
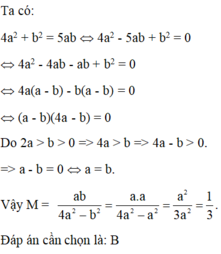
4a^2 + b^2=5ab
<=>4a^2 + b^2 - 5ab=0
<=>4a(a - b) - b(a - b)=0
<=> (a -b )(4a - b)=0
<=>a-b=0 ; a=b hoặc 4a - b=0 ; a=b/4(loại)
đề lúc đầu sai :v
ĐKXĐ : \(2a\ne b\)\(;\)\(2a\ne-b\)
\(4a^2+b^2=5ab\)\(\Leftrightarrow\)\(\left(a-b\right)\left(4a-b\right)=0\)\(\Leftrightarrow\)\(\orbr{\begin{cases}a-b=0\\4a-b=0\end{cases}\Leftrightarrow\orbr{\begin{cases}a=b\\4a=b\end{cases}}}\)
+) Với \(a=b\)\(\Rightarrow\)\(M=\frac{ab}{4a^2-b^2}=\frac{a^2}{4a^2-a^2}=\frac{a^2}{3a^2}=\frac{1}{3}\)
+) Với \(4a=b\)\(\Rightarrow\)\(M=\frac{ab}{4a^2-b^2}=\frac{a.4a}{4a^2-16a^2}=\frac{4a^2}{-12a^2}=\frac{-1}{3}\)
...
ĐKXĐ : \(a\ne b\)\(;\)\(a\ne-b\)
\(4a^2+b^2=5ab\)
\(\Leftrightarrow\)\(\left(4a^2-4ab\right)-\left(ab-b^2\right)=0\)
\(\Leftrightarrow\)\(4a\left(a-b\right)-b\left(a-b\right)=0\)
\(\Leftrightarrow\)\(\left(a-b\right)\left(4a-b\right)=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}a-b=0\\4a-b=0\end{cases}\Leftrightarrow\orbr{\begin{cases}a=b\left(loai\right)\\4a=b\end{cases}}}\)
\(\Rightarrow\)\(4a=b\)
\(\Rightarrow\)\(M=\frac{ab}{a^2-b^2}=\frac{a.4a}{\left(a-b\right)\left(a+b\right)}=\frac{4a^2}{\left(a-4a\right)\left(a+4a\right)}=\frac{4a^2}{-15a^2}=\frac{-4}{15}\)
...
Sửa lại đề bài: 1 / 2a- b
( MÁY MK KO ĐÁNH ĐC PHÂN SỐ MONG BN THÔNG CẢM)
mới lm đc nhé bn!
a) ĐKXĐ: bn tự lm nhé !
bn biến đổi: 2a3-b+2a-a2b = (2a-b) + ( 2a3-a2b) = (2a-b) + a2(2a-b) = (2a-b)(a2+1)
rồi bn nhân 1 / 2a+b với a2+1 rồi trừ 2 phân thức với nhau sẽ ra 0 => A=0
