Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Giả sử \(D\)không nằm giữa 2 điểm \(A\)và \(C\).
\(8=AC+BD\le CB=5\)(vô lí).
Do đó \(D\)nằm giữa 2 điểm \(A\)và \(C\).
b) \(AC+BD=AD+DC+BD=\left(AD+BD\right)+CD=AB+CD\)
\(\Rightarrow CD=AC+BD-AB=8-5=3\left(cm\right)\).

a)
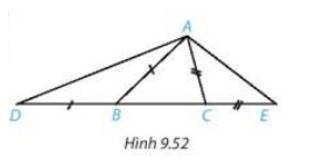
\(AB > AC \Rightarrow \widehat {ABC} < \widehat {ACB}\)( quan hệ giữa góc và cạnh đối diện trong tam giác ABC)
\(\begin{array}{l} \Rightarrow {180^0} - \widehat {ABD} < {180^0} - \widehat {ACE}\\ \Rightarrow \widehat {ABD} > \widehat {ACE}\end{array}\)
Vì BD= BA nên tam giác ABD cân tại B \( \Rightarrow \widehat {ABD} = {180^0} - 2\widehat {ADB}\)
Vì CE = CA nên tam giác ACE cân tại C \( \Rightarrow \widehat {ACE} = {180^0} - 2\widehat {AEC}\)
\(\begin{array}{*{20}{l}}{ \Rightarrow {{180}^0} - 2\widehat {ADB} > {{180}^0} - 2\widehat {AEC}}\\{ \Rightarrow \widehat {ADB} < \widehat {AEC}}\\{Hay{\mkern 1mu} \widehat {ADE} < \widehat {AED}}\end{array}\)
b) Xét tam giác ADE ta có : \(\widehat {ADB} < \widehat {AEC}\)
\( \Rightarrow AD > AE\)(Quan hệ giữa cạnh và góc đối diện trong tam giác).

a: OB<OC
=>B nằm giữa O và C
b: OA<OB
=>A nằm giữa O và B
mà B nằm giữa O và C
nên B nằm giữa A và C
c: A nằm giữa O và B
=>OA+AB=OB
=>AB=2cm
B nằm giữa O và C
=>OB+BC=OC
=>BC=1cm

Kí hiệu tam giác vt là t/g nhé
a) Xét t/g AOC và t/g BOD có:
OA = OB (gt)
CAO = DBO (gt)
AC = BD (gt)
Do đó, t/g AOC = t/g BOD (c.g.c)
=> OC = OD (2 cạnh tương ứng) (1)
Tương tự ta cũng có t/g AOE = t/g BOF (c.g.c)
=> OE = OF (2 cạnh tương ứng) (2)
(1) và (2) là đpcm
b) t/g AOC = t/g BOD (câu a)
=> AOC = BOD (2 góc tương ứng)
Mà AOC + COB = 180o ( kề bù)
nên BOD + COB = 180o
=> COD = 180o
=> C,O,D thẳng hàng
trường hợp c` lại tương tự
c) Có: AC = BD (gt); AE = BF (gt)
=> AE - AC = BF - BD ( vì hình của mk AE > AC c` nếu hình bn vẽ AC > AE thì ngược lại)
=> EC = FD
Vì BAx = ABy mà 2 góc này ở vị trí so le trong nên Ax // By
Xét t/g CEO và t/g DFO có:
CEO = DFO (so le trong)
EC = FD (cmt)
ECO = FDO (so le trong)
Do đó, t/g CEO = t/g DFO (g.c.g)
=> CO = DO (2 cạnh tương ứng)
EO = FO (2 cạnh tương ứng)
Từ đó dễ dàng suy ra t/g COF = t/g DOE (c.g.c)
=> CF = DE (2 cạnh tương ứng) (đpcm)


Gọi I là trung điểm của BC
Trên tia đối của IM lấy điểm N sao cho IM = IN
Dễ chứng minh \(\Delta\)IAM = \(\Delta\)IDN (c.g.c) nên MA = MD (hai cạnh tương ứng) (1)
C nằm trong \(\Delta\)MDN nên MC + CN < MD + ND (2)
Thật dễ dàng khi c/m: \(\Delta\)IBM = \(\Delta\)ICN (c.g.c) => MB = NC (hai cạnh tương ứng) (3)
Từ (1), (2) và (3) suy ra MA + MD > MB + MC (đpcm)