Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}=\dfrac{1}{R}+\dfrac{1}{R}+\dfrac{1}{R}=\dfrac{3}{R}\\ \Rightarrow R_{tđ}=\dfrac{R}{3}\)
Đề chưa rõ lắm nhé, bạn dựa vào để tính ...

Cho ba điện trở R1 = R2 = R3 = R mắc song song với nhau. Điện trở tương đương đương Rtđ của đoạn mạch đó có thể nhận giá trị nào trong các giá trị
A. Rtđ = R.
B. Rtđ = 2R.
C. Rtđ = 3R.
D. Rtđ = R/3
Giải thích:
\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}=\dfrac{1}{R}+\dfrac{1}{R}+\dfrac{1}{R}=\dfrac{3}{R}\)
\(\Rightarrow R_{tđ}=\dfrac{R}{3}\Omega\)
Chọn D.

Cho ba điện trở R1 = R2 = R3 = R mắc song song với nhau . Điện trở tương đương Rtđ của đoạn mạch đó có thể giá trị nào trong các giá trị .
A. Rtđ = R
B. Rtđ =2R
C. Rtđ = 3R
D. Rtđ = R/3

\(R_1//R_2\)\(\Rightarrow\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}\Rightarrow\dfrac{1}{2,4}=\dfrac{1}{6}+\dfrac{1}{R_1}\)
\(\Rightarrow R_1=4\Omega\)
Ta có \(R_{td}=\dfrac{R_1R_2}{R_1+R_2}\) \(\Leftrightarrow2,4=\dfrac{R_16}{R_1+6}\Leftrightarrow2,4\left(R_1+6\right)=6R_1\)
\(\Leftrightarrow2,4R_1+14,4=6R_1\Leftrightarrow-3,6R_1=-14,4\Rightarrow R_1=4\Omega\)
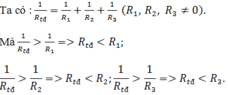
\(R_{tđ}=\dfrac{R_1\cdot R_2\cdot R_3\cdot R}{R_1+R_2+R_3+R}\)
\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}=\dfrac{1}{R}\\ \Rightarrow R_{tđ}=\dfrac{R_1.R_2.R_3.R}{R_1.R_2.R_3+R_1.R_2.R+R_1.R_3.R+R_2.R_3.R}\)