Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A E X B C K O I D F
Dễ chứng minh \(\Delta AEB\Delta ACE\left(g.g\right)\)
b ) Cm tứ giác \(OEAI\) và \(AEOF\) nt
Dễ thấy : \(\widehat{AEO}=\widehat{AIO}=90^o\)
\(\Rightarrow\) tứ giác OEAI nt đường tròn đường kính OA (1)
Lại có : \(\widehat{AEO}=\widehat{AFO}=90^o\)
\(\Rightarrow\) tứ giác AEOF nt đường tròn đường kính OA (2)
Từ (1) và (2) \(\Rightarrow\) đpcm
+ ) CM : ED//AC
Có : \(\widehat{xED}=\widehat{EFD}\left(=\frac{1}{2}sđcungED\right)\)
Mà 5 diểm A , E, O , I , F cùng thuộc 1 đường tròn
\(\Rightarrow\widehat{EFD}=\widehat{EAI}\left(=\frac{1}{2}sđEI\right)\)
\(\Rightarrow\widehat{xED}=\widehat{EAI}\)
\(\Rightarrow\) DE//AC
Chúc bạn học tốt !!!

2 tam giác HIE và HFA đồng dạng do có góc tại đỉnh H bằng nhau và góc HIE = góc FA (cùng chắn cung A của Q) => HI / HF = HE / HA => HI*HA = HE*HF ♦
2 ∆ HEB và HCF đồng dạng do có góc tại đỉnh H bằng nhau và góc HEB = góc HCF (cùng chắn cung BF của O) => HE / HC = HB / HF => HB*HC = HE*HF ♥
(Nếu bạn đã học phương tích của điểm đối với đường tròn thì có ngay ♦ và ♥ không cần cm vì ♦ chính là pt của H đối với Q còn ♥ là pt của H đối với O)
♦, ♥ => HI*HA = HB*HC => HI*(AI - HI) = (x - HI)(x + HI) => HI*AI = x²
=> HI = x² / AI = hằng số (A, I cố định nên AI không đổi)
=> H cố định.
Dễ thấy OIHK nội tiếp đường tròn (P) => đường tròn ngoại tiếp ∆ IOK chính là (P). Tâm đường tròn (P) dĩ nhiên nằm trên trung trực k của HI mà trung trực này cố định do H, I cố định. Vậy tâm đường tròn ngoại tiếp tam giác OIK luôn thuộc k cố định


gọi Ex là tia đối của tiếp tuyến EA
Ta có : \(\widehat{xED}=\frac{1}{2}sđ\widebat{ED}\); \(\widehat{EFD}=\frac{1}{2}sđ\widebat{ED}\)\(\Rightarrow\widehat{xED}=\widehat{EFD}\)( 1 )
Dễ thấy tứ giác AFOE nội tiếp
I là trung điểm của BC nên OI \(\perp\)BC \(\Rightarrow\)tứ giác AIOE nội tiếp
\(\Rightarrow\)5 điểm A,F,I,O,E cùng thuộc 1 đường tròn
\(\Rightarrow\)tứ giác AFIE nội tiếp \(\Rightarrow\)\(\widehat{EAI}=\widehat{EFI}\)( 2 )
Từ ( 1 ) và ( 2 ) suy ra : \(\widehat{xED}=\widehat{EAI}\Rightarrow ED//AC\)
Gọi N là giao điểm của AO và EF
Dễ chứng minh AN \(\perp\)EF
\(\DeltaẠNH~\Delta AIO\left(g.g\right)\Rightarrow\frac{AN}{AH}=\frac{AI}{AO}\Rightarrow AI.AH=AN.AO\)( 3 )
Ta có : \(AE^2=AN.AO\)( 4 )
Xét \(\Delta AEB\)và \(\Delta ACE\)có :
\(\widehat{EAC}\)( chung ) ; \(\widehat{AEB}=\widehat{ACE}=\frac{1}{2}sđ\widebat{EB}\)
\(\Rightarrow\Delta AEB~\Delta ACE\left(g.g\right)\)
\(\Rightarrow\frac{AE}{AB}=\frac{AC}{AE}\Rightarrow AE^2=AB.AC\)( 5 )
Từ ( 3 ) , ( 4 ) và ( 5 ) suy ra : AH.AI = AB.AC
đề bạn cho thiếu nhé. đoạn cuối AH. AI = AB . AC với H là giao điểm của AC và EF

a: Xét tứ giác ODAE có
góc ODA+góc OEA=180 độ
=>ODAE là tứ giác nội tiếp
b: \(AE=\sqrt{\left(3R\right)^2-R^2}=2\sqrt{2}\cdot R\)
\(OI=\dfrac{OE^2}{OA}=\dfrac{R^2}{3R}=\dfrac{R}{3}\)
c: Xét ΔDIK vuông tại I và ΔDHE vuông tại H có
góc IDK chung
=>ΔDIK đồng dạng vơi ΔDHE
=>DI/DH=DK/DE
=>DH*DK=DI*DE=2*IE^2

Bài 4:
a:
Xét (O) có
ΔCED nội tiếp
CD là đường kính
=>ΔCED vuông tại E
ΔOEF cân tại O
mà OI là đường cao
nên I là trung điểm của EF
Xét tứ giác CEMF có
I là trung điểm chung của CM và EF
CM vuông góc EF
=>CEMF là hình thoi
=>CE//MF
=<MF vuông góc ED(1)
Xét (O') có
ΔMPD nội tiêp
MD là đường kính
=>ΔMPD vuông tại P
=>MP vuông góc ED(2)
Từ (1), (2) suy ra F,M,P thẳng hàng
b: góc IPO'=góc IPM+góc O'PM
=góc IEM+góc O'MP
=góc IEM+góc FMI=90 độ
=>IP là tiếp tuyến của (O')

b: Xet ΔAEH và ΔACE có
góc AEH=góc ACE
góc EAH chung
=>ΔAEH đòng dạng vói ΔACE
=>AE^2=AH*AC
Xét ΔAEB và ΔACE có
góc AEB=góc ACE
góc EAB chung
=>ΔAEB đồng dạng với ΔACE
=>AE^2=AB*AC
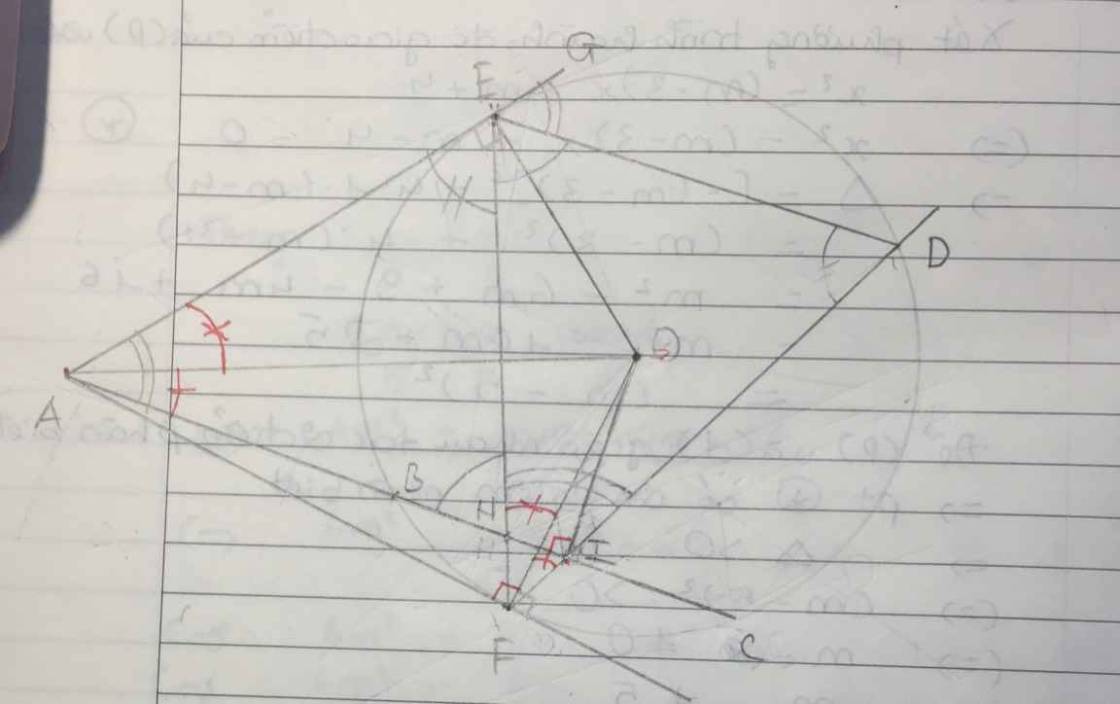
. . A B C D E F I K O x
a) Dễ cm: \(\Delta AEB~\Delta ACE\left(g.g\right)\)
b) cm: tứ giác OEAI và AEOF nt
Dễ thấy: \(\widehat{AEO}=\widehat{AIO}=90^0\)
=> tứ giác OEAI nt đường tròn đường kính OA (1)
Lại có: \(\widehat{AEO}=\widehat{AFO}=90^0\)
=> tứ giác AEOF nt đường tròn đường lính OA (2)
Từ (1)(2) =>đpcm
+) CM: ED//AC
Có: \(\widehat{xED}=\widehat{EFD}\left(=\frac{1}{2}sđcungED\right)\)
Mà 5 điểm A,E,O,I,F cùng thuộc 1 đường tròn
=> \(\widehat{EFD}=\widehat{EAI}\left(=\frac{1}{2}sđEI\right)\)
=>\(\widehat{xED}=\widehat{EAI}\)
=> DE//AC
p/s: hình ảnh chỉ mang t/c minh họa