Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đúng
Giải thích: Nhận thấy a→ = -3.i→
Vì –3 < 0 nên a→ và i→ ngược hướng.
b) Đúng.
Giải thích:
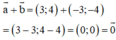
⇒ a→ = -b→ nên a→ và b→ là hai vec tơ đối nhau.
c) Sai
Giải thích:
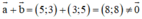
⇒ a→ ≠ -b→ nên a→ và b→ không phải là hai vec tơ đối nhau.
d) Đúng
Nhận xét SGK : Hai vec tơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau.

Đáp án:
AD+BC
=ED-EA+EC-EB
=(ED+EC)-(EA+EB) (1)
Mà E là trung điểm của AB=> EA+EB=0
(1)=2EF (F là trung điểm DC)

a) Vẽ trục và biểu diễn các điểm

b) Ta có:
A có tọa độ là –1, B có tọa độ là 2 nên 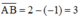
M có tọa độ là 3, N có tọa độ là –2 nên 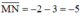


\(a,\) \(\overrightarrow{BC}=\left(4;-2\right)\Rightarrow BC=\sqrt{4^2+\left(-2\right)^2}=2\sqrt{5}\)
\(b,\) P là trung điểm AB
\(\left\{{}\begin{matrix}x_P=\dfrac{x_A+x_B}{2}=\dfrac{1-1}{2}=0\\y_P=\dfrac{y_A+y_B}{2}=\dfrac{-2+4}{2}=1\end{matrix}\right.\)
\(\Rightarrow P\left(0;1\right)\)
\(CP\left\{{}\begin{matrix}quaC\left(3;2\right)\\VTCP\overrightarrow{CP}=\left(-3;-1\right)\Rightarrow VTPT\overrightarrow{n}=\left(1;-3\right)\end{matrix}\right.\)
\(PTTQ\) của \(CP:1\left(x-3\right)-3\left(y-2\right)=0\)
\(\Leftrightarrow x-3-3y+6=0\)
\(\Leftrightarrow x-3y+3=0\)
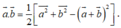




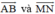 . Từ đó suy ra hai vec tơ
. Từ đó suy ra hai vec tơ 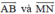 ngược hướng.
ngược hướng.
Chọn C.
Phương án A : biểu thức tọa độ tích vô hướng nên loại A.
Phương án B : Công thức tích vô hướng của hai véc tơ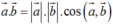 nên loại B.
nên loại B.
Phương án C: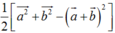
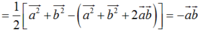 nên chọn C.
nên chọn C.