Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có \(\left\{{}\begin{matrix}\widehat{O_1}+\widehat{O_2}=180^0\left(kề.bù\right)\\\widehat{O_3}+\widehat{O_4}=180^0\left(kề.bù\right)\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\widehat{O_2}=180^0-140^0=40^0\\\widehat{O_4}=180^0-130^0=150^0\end{matrix}\right.\)
\(\widehat{AOB}=\widehat{O_2}+\widehat{O_4}=40^0+50^0=90^0\\ \Rightarrow OA\perp OB\)

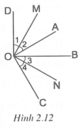
Ta có O C ⊥ O A ⇒ A O C ^ = 90 ° . O D ⊥ O B ⇒ B O D ^ = 90 ° .
Tia OB nằm giữa hai tia OA, OC.
Do đó A O B ^ + B O C ^ = 90 ° . (1)
Tương tự, ta có A O B ^ + A O D ^ = 90 ° . (2)
Từ (1) và (2) ⇒ B O C ^ = A O D ^ (cùng phụ với A O B ^ ).
Tia OM là tia phân giác của góc AOD ⇒ O 1 ^ = O 2 ^ = A O D ^ 2 .
Tia ON là tia phân giác của góc BOC ⇒ O 3 ^ = O 4 ^ = B O C ^ 2 .
Vì A O D ^ = B O C ^ nên O 1 ^ = O 2 ^ = O 3 ^ = O 4 ^ .
Ta có A O B ^ + B O C ^ = 90 ° ⇒ A O B ^ + O 3 ^ + O 4 ^ = 90 ° ⇒ A O B ^ + O 3 ^ + O 2 ^ = 90 ° .
Do đó M O N ^ = 90 ° ⇒ O M ⊥ O N