Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để A và B có nghĩa \(\Rightarrow\left\{{}\begin{matrix}m-4\le1\\m>-3\end{matrix}\right.\) \(\Rightarrow-3< m\le5\)
\(A\cup B=B\Leftrightarrow A\subset B\)
\(\Rightarrow\left\{{}\begin{matrix}m-4>-3\\m\ge1\end{matrix}\right.\) \(\Rightarrow m>1\)
\(\Rightarrow1< m\le5\Rightarrow m=\left\{2;3;4;5\right\}\)
Tổng bằng ....

Điều kiện để A xác định là:
\(m-1< 8\)
\(\Leftrightarrow m< 8+1\Leftrightarrow m< 9\)
Để: \(A\backslash B=\varnothing\)
\(\Leftrightarrow A\subset B\) \(\Rightarrow2\le m-1\)
\(\Leftrightarrow m\ge3\)
kết hợp với điều kiện:
\(\Rightarrow3\le m< 9\)

a: Để B là tập con của A thì m-7>-4 và m<3
=>m>3 và m<3
=>\(m\in\varnothing\)
b: Để A hợp B=A thì B là tập con của A
=>-3>-4 và m<=1
=>m<=1
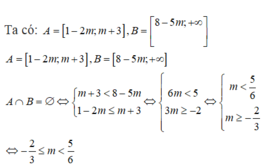
Để tập hợp A và B có nghĩa thì:
\(m-4\le1\Leftrightarrow m\le5\) (1)
\(m>-3\) (2)
Từ (1) và (2) \(\Rightarrow-3< m\le5\)
Mà: \(A\cup B=B\)
\(\Rightarrow A\subset B\)
\(\Rightarrow\left\{{}\begin{matrix}m-4>-3\\m\ge1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>-3+4\\m\ge1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>1\\m\ge1\end{matrix}\right.\Leftrightarrow m>1\)
Mà: \(-3< m\le5\)
\(\Rightarrow1< m\le5\)
\(\Rightarrow m=\left\{2;3;4;5\right\}\)
Tổng là: có 4 giá trị m nguyên thỏa mãn
Bạn ơi hình như bạn thiếu tổng tất cả giá trị của m là: 2 + 3 + 4 + 5 = 14?