Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

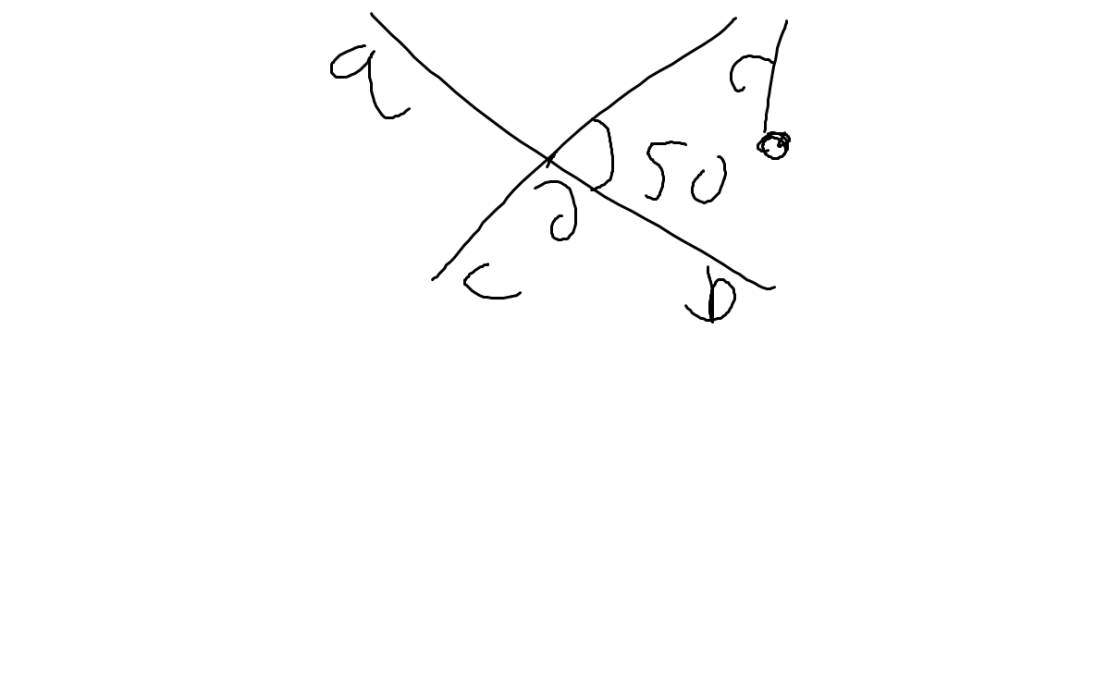
Gọi hai đường thẳng đề bài cho là ab và cd. Gọi O là giao của ab và cd
a: góc bOd và góc aOc
góc aOd và góc bOc
b: góc aOc=góc bOd=50 độ
góc aOd=góc bOc=180-50=130 độ

Gọi hai đường thẳng cắt nhau là xx' và yy'. Gọi điểm cắt giữa hai đường thẳng là O
a/ Các cặp góc đối đỉnh là: góc xOy đối đỉnh với góc y'Ox' ; góc x'Oy đối đỉnh với góc xOy'
b/ Gọi góc xOy = 50o
Vì góc xOy đối đỉnh với góc y'Ox'
suy ra góc xOy = y'Ox' = 50o
Vì hai đường thẳng xx' và yy' cắt nhau tại O
Suy ra tia Ox và tia Ox' đối nhau ; tia Oy và tia Oy' là hai tia đối nhau
Suy ra góc xOy và góc yOx' kề bù
Suy ra góc xOy + góc yOx' = 180o
50o + góc yOx' = 180o ( vì góc xOy = 50o )
góc yOx' = 180o - 50o = 130o
Vì góc yOx' và góc xOy' là hai góc đối đỉnh
Suy ra góc yOx' = góc xOy' = 130o
Vậy: ........... ( bạn tự viết nhé )
Nhớ k cho mình nhé! Thank you!!!

1,
Ta có : xOz + zOy = 180 độ( kề bù)
hay: xOz +47độ= 180 độ
xOz = 180 độ - 47 độ = 133độ.
2)
- Hai góc vuông không đối đỉnh là : góc xAy và góc x'Ax.
3)
4)
- các góc bằng nhau là :O1=O4 ; O2 = O5 ; O3 = z'Ox' ( đối đỉnh)
( viết số vào chân bên phải của góc và viết đúng kí hiệu góc , độ nka)

a) Vì \(MOP-MOQ\) là hai góc kề bù, ta có :
\(MOQ=180^0_{ }-MOP=180^0_{ }-70^0_{ }\)
\(\Rightarrow MOQ=110^0_{ }\)
Áp dụng tính chất hai góc đối đỉnh, ta có :
\(MOP=NOQ\)
\(MOQ=PON\)
b) Vì \(Ot\) là tia phân giác của \(MOP\Rightarrow TOP=TOM=\frac{1}{2}MOP=\frac{110}{2}=55^0_{ }\)
Vì \(POT-QOT'\) là hai góc đối đỉnh \(\Rightarrow POT=QOT'=55^0_{ }\left(1\right)\)
Vì \(MOT-NOT'\)là hai góc đối đỉnh \(\Rightarrow MOT=NOT'=55^0_{ }\left(2\right)\)
Từ \(\left(1\right)-\left(2\right)\Rightarrow OT'\)là tia phân giác của \(NOQ\)
c) \(POT-QOT'\)
\(MOT-NOT'\)
\(POM-NOQ\)

a)
b) \(\widehat{A_3}=\widehat{B_3}=130^o\) ( đồng vị; a//b)
c) \(\widehat{A_3}=\widehat{B_1}=130^o\) ( so le trong; a//b)
d)Cặp góc trong cùng phía là: \(\widehat{A_3}\) và \(\widehat{B_2}\)
Vì \(\widehat{A_3}\) và \(\widehat{B_2}\) là hai góc trong cùng phía:
nên: \(\widehat{A_3}+\widehat{B_2}=130^o+50^o=180^o\)
Vậy \(\widehat{A_3}+\widehat{B_3}=180^o\)
![]() ^...^
^...^ ![]() ^_^ ( Bài mk làm có gì ko hiểu bạn cứ hỏi mk nhé)
^_^ ( Bài mk làm có gì ko hiểu bạn cứ hỏi mk nhé)

Giả sử hai đường thẳng \(xx'\)và \(yy'\)cắt nhau tại O và \(\widehat{xOy}=47^0\)
\(\Rightarrow\widehat{x'Oy'}=\widehat{xOy}=47^0\)đối đỉnh
\(\widehat{xOy'}=180^0-\widehat{xOy}=180^0-47^0=133^0\)
do \(\widehat{xOy}\)và \(\widehat{xOy'}\)kề bù và \(\widehat{x'Oy}=\widehat{xOy'}=133^0\)
Bài 2 : Ta có hình vẽ :
Các cặp góc bằng nhau là : \(\widehat{xOy}=\widehat{x'Oy'};\widehat{yOz}=\widehat{y'Oz'}\)
AOBAOB^ và ˆDOCDOC^ là hai góc đối đỉnh.
ˆAODAOD^ và ˆBOCBOC^ là hai góc đối đỉnh.
Giả sử ˆAOB=500AOB^=500
Cần tính số đo các góc AOD, DOC, BOC.
Hai góc AOB và AOD là hai góc kề bù.
⇒ˆAOB+ˆAOD=1800⇒AOB^+AOD^=1800
Do đó: ˆAOD=1800–500=1300AOD^=1800–500=1300
Ta có: ˆDOC=ˆAOBDOC^=AOB^ (hai góc đối đỉnh) nên ˆDOC=500DOC^=500
Mặt khác ˆBOC=ˆAODBOC^=AOD^ (hai góc đối đỉnh) nên ˆBOC=1300
Nhìn vào hình , ta thấy :
O1 đối đỉnh với O3
O2 đối đỉnh với O4
Vì O1 và O3 là 2 góc đối đỉnh ( ở trên )
=> O1 = O3 mà O1 = 50o ( bài cho )
=> O3 = 50o
Vì O1 và O2 là hai góc kề bù ( bài cho )
=> O1 + O2 = 180o mà O1 = 50o ( bài cho )
=> O2 = 180o - 50o = 130o mà O2 và O4 là 2 góc đối đỉnh ( ở trên )
=> O2 = O4 => O4 = 130o