Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải :
Hình vẽ ; giả thiết, kết luận đã được đầu bài cho sẵn.
Chứng minh :
Xét \(\Delta AMC\text{ và }\Delta BMD\), có :
\(MA=MB\text{ (gt)}\)
\(\angle AMC=\angle DMB\text{ (đối đỉnh)}\)
\(DM=CM\text{ (gt)}\)
\(\Rightarrow\Delta AMC=\Delta BMD\text{ (c.g.c)}\)
b/ Ta có : \(\bigtriangleup AMC=\bigtriangleup BMD\text{ (c.m.t)}\)
\(\Rightarrow\widehat{DBM}=\widehat{ACM}\text{ (2 góc tương ứng ở vị trí so le trong)}\) (1)
\(\Rightarrow BD//AC\)
Xét \(\bigtriangleup DMA\text{ và }\bigtriangleup BMC,\text{ có :}\)
\(\widehat{DMA}=\widehat{BMC}\text{ (đối đỉnh)}\)
\(DM=CM\left(gt\right)\)
\(BM=AM\left(gt\right)\)
\(\Rightarrow\bigtriangleup DMA=\bigtriangleup BMC\left(c.g.c\right)\)
\(\Rightarrow\widehat{ADM}=\widehat{DCM}\text{ (2 góc tương ứng ở vị trí so le trong)}\) (2)
\(\text{Từ (1) và (2) suy ra tứ giác ABCD là hình bình hành}\) (3)
\(\angle ACB=90^{\text{o}}\) (4)
\(\text{T}ừ\text{ (3) và (4) suy ra hình bình hành ABCD là hình chữ nhật}\) (đpcm)

Bài 1: Tính B = 1 + 2 + 3 + ... + 98 + 99
Số số hạng của B là : 99 số hạng
Tổng của B là ( 1 + 99 ) x 99 : 2 = 4950
Vậy : B = 1 + 2 + 3 + ... + 98 + 99 = 4950
Bài 2: Tính C = 1 + 3 + 5 + ... + 997 + 999
Số số hạng của C là : ( 999 - 1 ) : 2 + 1 = 500 ( số hạng )
Tổng của C là : ( 1 + 999 ) x 500 : 2 = 250000
Bài 3. Tính D = 10 + 12 + 14 + ... + 994 + 996 + 998
Số số hạng của D là : ( 998 - 10 ) : 2 + 1 = 495 ( số hạng )
Tổng của D là : ( 10 + 998 ) x 495 : 2 = 249480
!)
B=1+2+3+...+98+99
B= 99(99+1):2
B = 4950
( Áp dụng: Nếu B=1+2+3+...+(n-1)+n
thì B=n(n+1):2
B=4950 nha bạn!
2) Tính: C=1+3+5+...+997+999
Ta có: 999= 2(500)-1. n=500
1+2+3+...+(2n-1)= n^2
= 500^2= 250.000
C=25.000


câu này mình vừa làm ở bạn Khang Phạm Duy , HÂN nhé
tham khảo .mình giải rất chi tiết

a) 1cm + 2cm = 3cm < 4cm
⇒ bộ ba đoạn thẳng 1cm, 2cm, 4cm không thể tạo thành 1 tam giác.
b) 2cm + 3cm = 5cm.
⇒ Bộ ba đoạn thẳng 2cm; 3cm; 5cm không lập thành tam giác.
c) Ta có 3cm + 4cm = 7cm > 5cm.
Do đó bộ đoạn thẳng 3cm, 4cm, 5cm có thể thành 3 cạnh của tam giác.
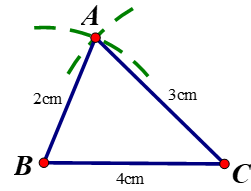
Cách dựng tam giác có ba độ dài 3cm, 4cm, 5cm :
- Vẽ BC = 4cm
- Dựng đường tròn tâm B bán kính 2cm ; đường tròn tâm C bán kính 3cm. Hai đường tròn cắt nhau tại A. Nối AB, AC ta được tam giác cần dựng.

Lũy thừa và công thức lũy thừa
I. Lũy thừa với số mũ nguyên :
1. Lũy thừa với số mũ tự nhiên : Cho \(a\inℝ,\: n\inℕ\). Khi đó :
a n = a.a.a...a n số a
2. Lũy thừa với số mũ nguyên âm : Cho \(a\inℝ^+,\: n\inℕ^+\). Khi đó : \(a^{-n}=\frac{1}{a^n}\:\text{và}\:a^0=1\).
Chú ý : 0 và 0 không có nghĩa. 0 -n
II. Lũy thừa với số mũ hữu tỉ :
Cho a > 0 và số hữu tỉ : \(r=\frac{m}{n}\) ; trong đó \(m\inℤ,\:n\inℕ,\:n\ge2\) . Khi đó : \(a^r=a^{\frac{m}{n}}=\sqrt[n]{a^m}\).
III. Các tính chất :
1. Nhân 2 lũy thừa cùng cơ số : \(a^m\cdot a^n=a^{m+n}\).
2. Chia 2 lũy thừa cùng cơ số : \(a^m:a^n=a^{m-n}\).
3. Lũy thừa của 1 tích : \(\left(a\cdot b\right)^n=a^n\cdot b^n\).
4. Lũy thừa của 1 thương : \(\left(\frac{a}{b}\right)^n=\frac{a^n}{b^n}\).
5. Lũy thừa của lũy thừa : \(\left(a^m\right)^n=a^{m\cdot n}\).
6. Lũy thừa mũ lũy thừa : \(a^{m^n}=a^{\left(m^n\right)}\).
7. a1 = a.
8. a0 = 1.