Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
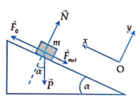
+ Khi vật trượt đều lên mặt phẳng nghiêng:
![]()
Chiếu lên phương mặt phẳng nghiêng và vuông góc với mặt phẳng nghiêng:
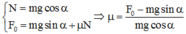
+ Khi vật trượt đều trên mặt ngang:
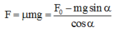

Chọn C.
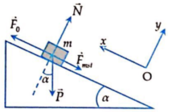
+ Khi vật trượt đều lên mặt phẳng nghiêng:
F 0 ⇀ + P ⇀ + N ⇀ + F m s ⇀ = 0 ⇀
Chiếu lên phương mặt phẳng nghiêng và vuông góc với mặt phẳng nghiêng:
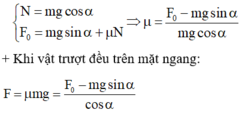

p=mg=20(N)
N=p.cos30
TA có Sin30=4/h ->h=8m
mặt khác Af=FScos0=160
+A/fms=MNScos180= -13,856
+Ap=p.s.cos(90-30)=80

để xe chuyển động đều (a=0)
\(\overrightarrow{F_k}+\overrightarrow{P}+\overrightarrow{N}=0\)
chiếu lên trục Ox song song với mặt phằng
Fk-sin\(\alpha\).P=0
\(\Rightarrow\)Fk=150N

a/ \(F_k-F_{ms}=m.a\Rightarrow\mu=\dfrac{F_k-m.a}{mg}=...\)
b/ \(F_k.\cos30^0-F_{ms}=m.a\Rightarrow\mu=\dfrac{F_k.\cos30^0-m.a}{mg}\)

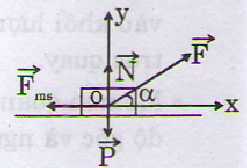
Lực tác dụng lên vật m được biểu diễn trên hình vẽ.
Định luật II Niu-tơn cho:
Chọn hệ trục Oxy với chiều dương là chiều chuyển động theo phương Ox, chiếu phương trình (1) lên:
(Ox): Fcosα- fms= ma (2)
(Oy): N + Fsinα – P = 0 (3)
mà fms= μN (4)
(2), (3) và (4) => F cosα – μ(P- Fsinα ) = ma
=> Fcosα – μP + μFsinα = ma
F(cosα +μsinα) = ma +μmg
=> F =
a) khi a = 1,25 m/s2

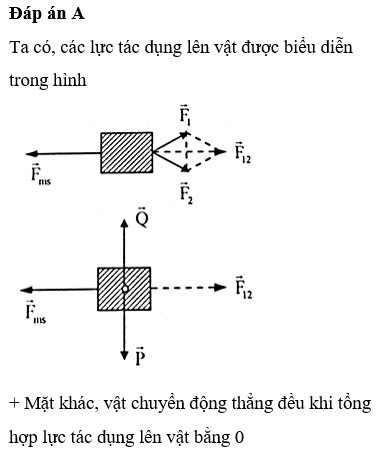
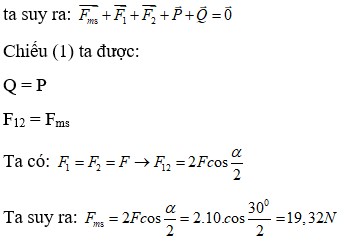

theo phương song song với mặt phẳng
\(cos\beta.F-\mu.N-sin\alpha.P=m.a\) (1)
theo phương vuông gốc với mp nghiêng
N=\(cos\alpha.P-sin\beta.F\) (2)
từ (1),(2)\(\Rightarrow F=\dfrac{m.a+P.\left(\mu.cos\alpha+sin\alpha\right)}{cos\beta-sin\beta.\mu}\) (a=0)
\(\Rightarrow F\approx29,72N\)