Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
\(y'=m-3cos3x\)
Hàm đồng biến trên R khi và chỉ khi \(m-3cos3x\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\ge3cos3x\) ; \(\forall x\)
\(\Leftrightarrow m\ge\max\limits_{x\in R}\left(3cos3x\right)\)
\(\Leftrightarrow m\ge3\)
2.
\(y'=1-m.sinx\)
Hàm đồng biến trên R khi và chỉ khi:
\(1-m.sinx\ge0\) ; \(\forall x\)
\(\Leftrightarrow1\ge m.sinx\) ; \(\forall x\)
- Với \(m=0\) thỏa mãn
- Với \(m< 0\Rightarrow\dfrac{1}{m}\le sinx\Leftrightarrow\dfrac{1}{m}\le\min\limits_R\left(sinx\right)=-1\)
\(\Rightarrow m\ge-1\)
- Với \(m>0\Rightarrow\dfrac{1}{m}\ge sinx\Leftrightarrow\dfrac{1}{m}\ge\max\limits_R\left(sinx\right)=1\)
\(\Rightarrow m\le1\)
Kết hợp lại ta được: \(-1\le m\le1\)

Gọi số đó là \(\overline{xyz}\). Theo đề bài, ta có \(2\left(yz+5\right)=x^2\) \(\Rightarrow x⋮2\)
Mà \(2\left(yz+5\right)\ge10\) nên \(x^2\ge10\Leftrightarrow x\ge4\)
\(\Rightarrow x\in\left\{4,6,8\right\}\)
Nếu \(x=4\) thì \(yz+5=8\Leftrightarrow yz=3\) \(\Rightarrow\left(y,z\right)\in\left\{\left(1;3\right),\left(3;1\right)\right\}\)
Nếu \(x=6\) thì \(yz+5=18\Leftrightarrow yz=13\), vô lí.
Nếu \(x=8\) thì \(yz+5=32\Leftrightarrow yz=27\) \(\Leftrightarrow yz\in\left\{\left(3;9\right),\left(9;3\right)\right\}\)
Vậy có 4 số thỏa mãn ycbt là 413, 431, 839, 893.

a) Đường phân giác của góc phần tư thứ nhất và góc pần tư thứ ba.
b) Đường phân giác của góc phần tư thứ hai và góc phần tư thứ tư.
c) Đường thẳng y = 2x + 1
d) Nửa đường tròn tâm O bán kính bằng 1, nằm bên phải trục Oy.

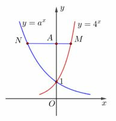
Đáp án C
Vì x = 1 là một nghiệm của bất phương trình
![]()
Khi đó, bất phương trình
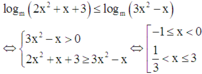
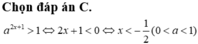
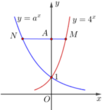
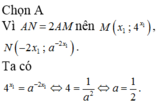
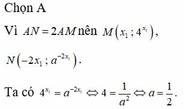
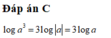
?????????????????????????????????????????????
Thiếu dữ kiện nha bạn
Mong bạn bổ sung