Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có: l = 1745,25m ± 0,01m có độ chính xác đến hàng phần trăm (độ chính xác là 0,01) nên ta quy tròn số đến hàng phần chục.
Vậy số quy tròn của 1745,25m là 1745,3 m.
Ta có h = 347,13 ± 0,2m có độ chính xác đến hàng phần chục (độ chính xác bằng 0,2) nên ta quy tròn số đến hàng đơn vị.
Số quy tròn của 347,13 là 347 m.
Ta có: l = 1745,25m ± 0,01m có độ chính xác đến hàng phần trăm (độ chính xác là 0,01) nên ta quy tròn số đến hàng phần chục.
Vậy số quy tròn của 1745,25m là 1745,3 m.
Vì độ chính xác đến hàng phần nghìn (độ chính xác là 0,001) nên ta quy tròn số 1,256 đến hàng phần trăm. Vậy số quy tròn của l là 1,26.
Đáp án A
Vì độ chính xác đến 10–10 (10 chữ số thập phân sau dấu ,) nên ta quy tròn đến 10–9 (9 chữ số thập phân sau dấu phẩy)
Vậy số quy tròn của a là 3,141592654.
Yêu cầu ở câu a) là quy tròn đến hàng phần trăm còn yêu cầu ở câu b) chỉ yêu cầu quy tròn tức là ta phải quy tròn số với độ chính xác đã cho.
Đáp án: D
Ta có sai số tuyệt đối của số đo chiều dài con dốc là :
Δa = a . δ a = 182,55. 0,2% = 0.3851.
Vì 0.05 < Δa < 0,5 . Do đó chữ số chắc của d là 1, 9, 2.
Vậy cách viết chuẩn của a là 193m (quy tròn đến hàng đơn vị).
Hàng của chữ số khác 0 đầu tiên bên trái của độ chính xác \(d = 100\) là hàng trăm, nên ta quy tròn \(a = 6547\) đến hàng nghìn.
Vậy số quy tròn của a là 7 000.
Ta có: \(6547-100<\overline a< 6547+100 \Leftrightarrow 6447 <\overline a< 6647\) nên \(6447-7000 <\overline a -7000< 6647-7000 \Leftrightarrow -553 <\overline a -7000< -353 \Rightarrow |\overline a -7000| < 553\)
Sai số tương đối là \({\delta _a} \le \frac{{553}}{{\left| {7000} \right|}} = 7,9\% \)
Độ chính xác của số đo là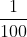
m. Chữ số 5 ở hàng phần trăm nên không đáng tin ta phải bỏ và theo quy tắc làm tròn.
Cộng thêm 1 đơn vị vào hàng kế tiếp (2+1=3).
Tóm lại các chữ số đáng tin là 1; 7; 4; 5; 2 và chiều dài cầu viết dưới dạng chuẩn là d= 1745,30.