Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(R_{23}=\dfrac{R_2\cdot R_3}{R_2+R_3}=\dfrac{10\cdot10}{10+10}=5\Omega\)
\(R_N=R_1+\dfrac{R_2\cdot R_3}{R_2+R_3}=6+\dfrac{10\cdot10}{10+10}=11\Omega\)
a)Cường độ dòng điện qua mạch chính:
\(I=\dfrac{\xi}{R_N+r}=\dfrac{12}{1+11}=1A\)
\(\Rightarrow I_{23}=I_1=1A\)\(\Rightarrow U_1=R_1\cdot I_1=1\cdot6=6V\)
\(U_{23}=I_{23}\cdot R_{23}=1\cdot5=5V\)\(\Rightarrow U_2=U_3=5V\)
\(I_2=\dfrac{5}{10}=0,5A;I_3=\dfrac{5}{10}=0,5A\)
b)ĐIện năng tiêu thụ mạch ngoài: \(A=U\cdot I\cdot t=\left(U_1+U_{23}\right)\cdot I_m\cdot t=\left(6+5\right)\cdot1\cdot10\cdot60=6600J\)


Độ lớn E: \(A=W\)\(\Rightarrow qEd=\dfrac{1}{2}mv_0^2\)
\((q=-1,6\cdot10^{-19},m=9,1\cdot10^{-31})\)
\(\Rightarrow E=-1,6\cdot10^{-7}\)V/m
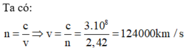
Vận tốc truyền của ánh sáng trong các môi trường tuân theo quy luật :
\(\frac{v_1}{v_2}=\frac{n_2}{n_1}\left(1\right)\)
Trong cùng thời gian thì quãng đường đi tỉ lệ với vận tốc nên :
\(\frac{v_1}{v_2}=\frac{s_1}{s_2}\left(2\right)\)
Từ (1) và (2) suy ra : \(\frac{s_1}{s_2}=\frac{n_2}{n_1}=\frac{4,42}{1,5}\approx1,6\)
Quãng đường ánh sáng đi được trong thủy tinh lớn gấp 1,6 lần quãng đường đi được trong kim cương.