K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
16 tháng 12 2023
a: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
=>OA=OC; OB=OD(1)
Ta có: P là trung điểm của OB
=>\(OP=PB=\dfrac{OB}{2}\left(2\right)\)
Ta có:Q là trung điểm của OD
=>\(OQ=QD=\dfrac{OD}{2}\left(3\right)\)
Từ (1),(2),(3) suy ra DQ=QO=OP=PB
Xét ΔMBP vuông tại M và ΔNDQ vuông tại N có
BP=DQ
\(\widehat{MBP}=\widehat{NDQ}\)(hai góc so le trong, MB//DN)
Do đó: ΔMBP=ΔNDQ
=>MP=NQ
Ta có: MP\(\perp\)AB
AB//CD
Do đó: MP\(\perp\)CD
Ta có: MP\(\perp\)CD
QN\(\perp\)CD
DO đó: MP//QN
Xét tứ giác PMQN có
PM//QN
PM=QN
Do đó: PMQN là hình bình hành
b:
Ta có: OP=OQ
P,O,Q thẳng hàng
Do đó: O là trung điểm của PQ
PMQN là hình bình hành
=>PQ cắt MN tại trung điểm của mỗi đường
mà O là trung điểm của PQ
nên O là trung điểm của MN
30 tháng 12 2023
Chi phí sản xuất mỗi chiếc xe đạp là 1,8 triệu đồng nên a=1,8
Chi phí cố định hoạt động hàng ngày là 36 triệu đồng nên b=36
Vậy: y=1,8x+36
26 tháng 8 2023
5:
a: \(-120x^5y^4=20x^5y^2\cdot\left(-6y^2\right)\)
b: \(60x^6y^2=20x^5y^2\cdot3x\)
c: \(-5x^{15}y^3=20x^5y^2\cdot\left(-\dfrac{1}{4}x^{10}y\right)\)
d: \(2x^{12}y^{10}=20x^5y^2\cdot\left(\dfrac{1}{10}x^7y^8\right)\)
HT
2
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 1
\(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
\(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(b+1\right)}=\dfrac{b}{a}\)
T
12 tháng 1
d) Để phân thức \(\dfrac{4x^3+4x^2}{x^2-1}\) có nghĩa thì: \(x^2-1\ne0\Leftrightarrow x\ne\pm1\)
Khi đó: \(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
e) Để phân thức \(\dfrac{b^2+b}{a+ab}\) có nghĩa thì: \(a+ab\ne0\Leftrightarrow a\ne-ab\)
Khi đó: \(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(1+b\right)}=\dfrac{b}{a}\)
T
28 tháng 1
\(N=\left(\dfrac{3x}{2x-2}-\dfrac{3x}{2x+2}-\dfrac{3x-2}{x^2-1}\right)\cdot\dfrac{4x^2-4}{3}\left(x\ne\pm1\right)\)
\(=\left[\dfrac{3x}{2\left(x-1\right)}-\dfrac{3x}{2\left(x+1\right)}-\dfrac{3x-2}{\left(x-1\right)\left(x+1\right)}\right]\cdot\dfrac{4x^2-4}{3}\)
\(=\left[\dfrac{3x\left(x+1\right)}{2\left(x-1\right)\left(x+1\right)}-\dfrac{3x\left(x-1\right)}{2\left(x-1\right)\left(x+1\right)}-\dfrac{2\cdot\left(3x-2\right)}{2\left(x-1\right)\left(x+1\right)}\right]\cdot\dfrac{4\left(x^2-1\right)}{3}\)
\(=\dfrac{3x^2+3x-3x^2+3x-6x+4}{2\left(x-1\right)\left(x+1\right)}\cdot\dfrac{4\left(x-1\right)\left(x+1\right)}{3}\)
\(=\dfrac{4\cdot2}{3}\)
\(=\dfrac{8}{3}\)
Vậy giá trị của \(N\) không phụ thuộc vào biến \(x\).
H
14 tháng 2
\(N=\left(\dfrac{3x}{2x-2}-\dfrac{3x}{2x+2}-\dfrac{3x-2}{x^2-1}\right)\cdot\dfrac{4x^2-4}{3}\\ =\left(\dfrac{3x}{2\left(x-1\right)}-\dfrac{3x}{2\left(x+1\right)}-\dfrac{3x-2}{\left(x-1\right)\left(x+1\right)}\right)\cdot\dfrac{4x^2-4}{3}\\ =\dfrac{3x\left(x+1\right)-3x\left(x-1\right)-2\left(3x-2\right)}{2\left(x-1\right)\left(x+1\right)}\cdot\dfrac{4x^2-4}{3}\\ =\dfrac{\left(3x^2+3x\right)-\left(3x^2-3x\right)-\left(6x-4\right)}{2\left(x-1\right)\left(x+1\right)}\cdot\dfrac{4x^2-4}{3}\)
\(=\dfrac{3x^2+3x-3x^2+3x-6x+4}{2\left(x-1\right)\left(x+1\right)}\cdot\dfrac{4\left(x-1\right)\left(x+1\right)}{3}\\ =\dfrac{4}{2\left(x-1\right)\left(x+1\right)}\cdot\dfrac{4\left(x-1\right)\left(x+1\right)}{3}\\ =\dfrac{4\cdot2}{3}\)
`=8/3`
`->N` không phụ thuộc vào biến `x`
`color{blue}{ @ A_ri}`
24 tháng 11 2023
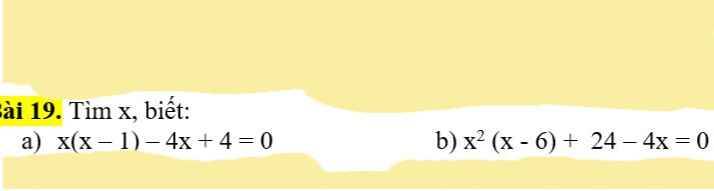
a: \(x\left(x-1\right)-4x+4=0\)
=>\(x\left(x-1\right)-\left(4x-4\right)=0\)
=>\(x\left(x-1\right)-4\left(x-1\right)=0\)
=>\(\left(x-1\right)\left(x-4\right)=0\)
=>\(\left[{}\begin{matrix}x-1=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=4\end{matrix}\right.\)
b: \(x^2\left(x-6\right)+24-4x=0\)
=>\(x^2\left(x-6\right)-\left(4x-24\right)=0\)
=>\(x^2\left(x-6\right)-4\left(x-6\right)=0\)
=>\(\left(x-6\right)\left(x^2-4\right)=0\)
=>\(\left(x-6\right)\left(x-2\right)\left(x+2\right)=0\)
=>\(\left[{}\begin{matrix}x-6=0\\x-2=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\x=2\\x=-2\end{matrix}\right.\)
4 tháng 12 2023
a: \(\left(x^2+x+1\right)\left(x^2+x+2\right)-12\)
\(=\left(x^2+x\right)^2+2\left(x^2+x\right)+\left(x^2+x\right)+2-12\)
\(=\left(x^2+x\right)^2+3\left(x^2+x\right)-10\)
\(=\left(x^2+x\right)^2+5\left(x^2+x\right)-2\left(x^2+x\right)-10\)
\(=\left(x^2+x\right)\left(x^2+x+5\right)-2\left(x^2+x+5\right)\)
\(=\left(x^2+x+5\right)\left(x^2+x-2\right)\)
\(=\left(x^2+x+5\right)\left(x^2+2x-x-2\right)\)
\(=\left(x^2+x+5\right)\left[x\left(x+2\right)-\left(x+2\right)\right]\)
\(=\left(x^2+x+5\right)\left(x+2\right)\left(x-1\right)\)
b: \(\left(x^2+2x\right)^2+9x^2+18x+20\)
\(=\left(x^2+2x\right)^2+9\left(x^2+2x\right)+20\)
\(=\left(x^2+2x\right)^2+4\left(x^2+2x\right)+5\left(x^2+2x\right)+20\)
\(=\left(x^2+2x\right)\left(x^2+2x+4\right)+5\left(x^2+2x+4\right)\)
\(=\left(x^2+2x+4\right)\left(x^2+2x+5\right)\)
c: \(\left(x+2\right)\left(x+4\right)\left(x+6\right)\left(x+8\right)+16\)
\(=\left(x+2\right)\left(x+8\right)\left(x+4\right)\left(x+6\right)+16\)
\(=\left(x^2+8x+2x+16\right)\left(x^2+6x+4x+24\right)+16\)
\(=\left(x^2+10x+16\right)\left(x^2+10x+24\right)+16\)
\(=\left(x^2+10x\right)^2+24\left(x^2+10x\right)+16\left(x^2+10x\right)+384+16\)
\(=\left(x^2+10x\right)^2+40\left(x^2+10x\right)+400\)
\(=\left(x^2+10x+20\right)^2\)
3 tháng 7 2022
Gọi số chi tiết máy tổ 1 và tổ 2 sản xuất được lần lượt là a,b
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=900\\\dfrac{11}{10}a+b=1010\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1100\\b=-200\left(loại\right)\end{matrix}\right.\)
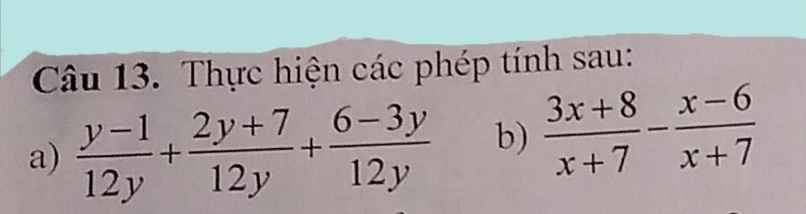
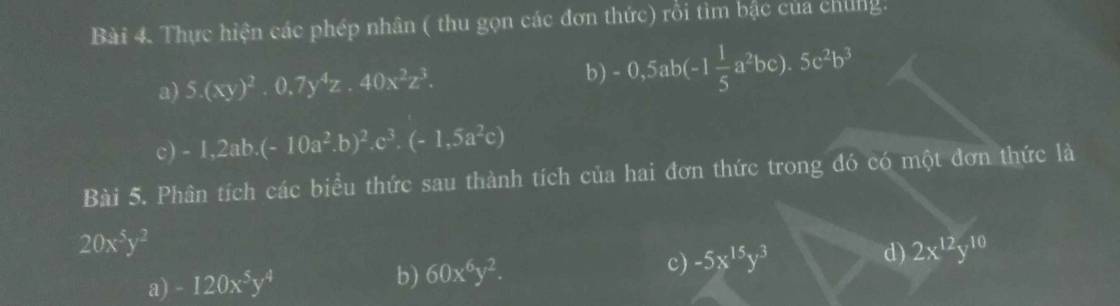
\(\dfrac{y-1}{12y}+\dfrac{2y+7}{12y}+\dfrac{6-3y}{12y}=\dfrac{y-1+2y+7+6-3y}{12y}=\dfrac{12}{12y}=\dfrac{1}{y}\)
\(\dfrac{3x+8}{x+7}-\dfrac{x-6}{x+7}=\dfrac{3x+8-\left(x-6\right)}{x+7}=\dfrac{3x+8-x+6}{x+7}=\dfrac{2x+14}{x+7}=\dfrac{2\left(x+7\right)}{x+7}=2\)