K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 7 2015
Gọi x là số chi tiết mà xưởng phải làm theo kế hoạch ( DK x > 0)
theo kế hoạch xưởng phải làm trong: x / 10 ngày
Thực tế mỗi ngày xưởng làm đc 16 chi tiết và đc thêm 4 chi tiết thừa 2 ngày nên mỗi ngày xuopwngr làm đc:
x+4/16 (ngày) và còn thừa 2 ngày
nên ta có pt;
x/10 - (x+4)/16 = 2
Đến đay bạn giải pt như bình thường
NHớ **** đấy
26 tháng 8 2023
5:
a: \(-120x^5y^4=20x^5y^2\cdot\left(-6y^2\right)\)
b: \(60x^6y^2=20x^5y^2\cdot3x\)
c: \(-5x^{15}y^3=20x^5y^2\cdot\left(-\dfrac{1}{4}x^{10}y\right)\)
d: \(2x^{12}y^{10}=20x^5y^2\cdot\left(\dfrac{1}{10}x^7y^8\right)\)
AH
Akai Haruma
Giáo viên
26 tháng 2 2022
Lời giải:
Gọi thời gian sản xuất theo kế hoạch là $a$ ngày
Số chi tiết máy sx theo kế hoạch: $48a$
Số chi tiết máy thực tế: $60(a-2)$
Theo bài ra: $60(a-2)-48a=12$
$\Leftrightarrow 12a=132$
$\Leftrightarrow a=11$ (ngày)
Số chi tiết máy sx theo kế hoạch: $48a=48.11=528$ (chi tiết máy)
NB
2 tháng 5 2023
gọi số chi tiết máy thực tế đội sx đc là x(chi tiết máy) (x ∈ N; x>60)
số chi tiết máy dự định của đội sx là x-60 (chi tiết máy)
thời gian đội sx hoàn thành theo dự định là \(\dfrac{x-60}{50}\) (ngày)
thời gian đội sx hoàn thành trong thực tế \(\dfrac{x}{60}\)
theo đề bài, đội hoàn thành xong trước kế hoạch 4 ngày nên ta có pt:
\(\dfrac{x-60}{50}\) - \(\dfrac{x}{60}\) = 4 (tự giải)
<=>x=1560(tmdk)
vậy số chi tiết máy thực tế đội sx đc là 1560 chi tiết máy
CM
26 tháng 11 2017
Gọi số chi tiết máy mà đội phải sản xuất theo kế hoạch là x (x ∈ N, x > 0)
Số chi tiết máy thực tế đội đã sản xuất được là x + 25
Số ngày hoàn thành công việc theo kế hoạch là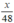 
(ngày)
Số ngày thực tế hoàn thành công việc là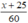 
(ngày)
Vì đội đã hoàn thành công việc xong trước 2 ngày so với kế hoạch nên ta có phương trình:
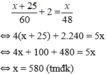
Vậy số chi tiết máy đội phải sản xuất theo kế hoạch là 580 chi tiết.
HT
2
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 1
\(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
\(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(b+1\right)}=\dfrac{b}{a}\)
T
12 tháng 1
d) Để phân thức \(\dfrac{4x^3+4x^2}{x^2-1}\) có nghĩa thì: \(x^2-1\ne0\Leftrightarrow x\ne\pm1\)
Khi đó: \(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
e) Để phân thức \(\dfrac{b^2+b}{a+ab}\) có nghĩa thì: \(a+ab\ne0\Leftrightarrow a\ne-ab\)
Khi đó: \(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(1+b\right)}=\dfrac{b}{a}\)
M
2
H
4 tháng 4 2021
Gọi số sản phẩm dự định là a (sản phẩm ) (a là số tự nhiên khác 0)
Vì theo dự định mỗi ngày sản xuất 50 sản phẩm nên số ngày theo dự định là \(\dfrac{a}{50}\)
Nhưng thực tế , đội đã sản xuất theeo được 30 sản phẩm do mỗi ngày vượt mức 10 sản phẩm (nghĩa là sản xuất 60 sản phẩm) , nên số ngày thực tế là \(\dfrac{a+30}{60}\)
Vì thực tế sớm hơn dự định 2 ngày nên ta có phương trình :
\(\dfrac{a}{50}=\dfrac{a+30}{60}+2\\ \Leftrightarrow6a=5\left(a+30+120\right)\\\Leftrightarrow a=750\left(t.m\right) \)
Vậy số sản phẩm dự định là 750 sản phẩm
4 tháng 4 2021
Bài 3:
Gọi số sản phẩm đội phải sản xuất theo kế hoạch là x( sản phẩm, x\(\in N\)*)
Thời gian đội sản xuất theo kế hoạch là: \(\dfrac{x}{50}\) (ngày)
Số ngày làm thực tế là: \(\dfrac{x+30}{50+10}=\dfrac{x+30}{60}\) (ngày)
Theo bài ra, ta có phương trình:
\(\dfrac{x}{50}-\dfrac{x+30}{60}=2\)
\(\Leftrightarrow\dfrac{60x-50\left(x+30\right)}{50.60}=2\)
\(\Leftrightarrow60x-50x-1500=6000\Leftrightarrow x=750\)(thoả mãn)
Vậy theo kế hoạch đội phải sản xuất 750 sản phẩm
VD
0
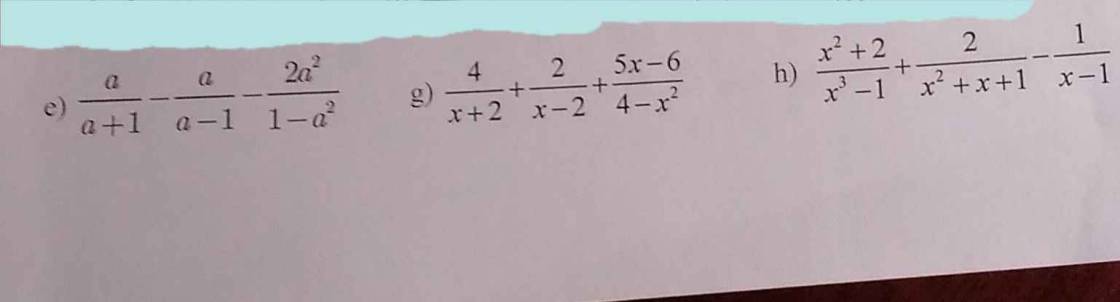
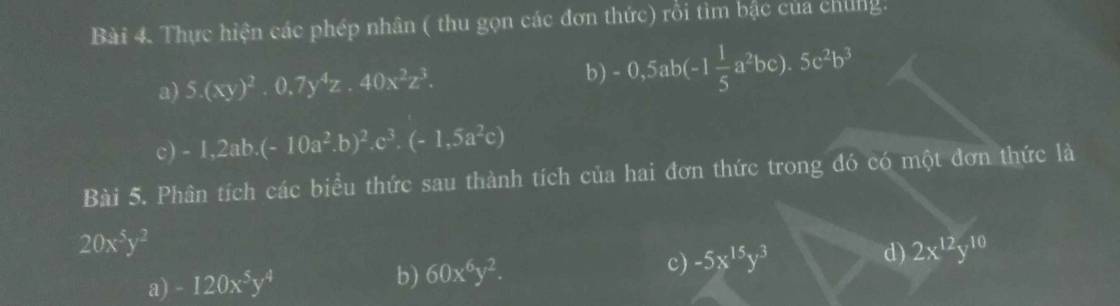
e: ĐKXĐ: \(a\notin\left\{-1;1\right\}\)
\(\dfrac{a}{a+1}-\dfrac{a}{a-1}-\dfrac{2a^2}{1-a^2}\)
\(=\dfrac{a}{a+1}-\dfrac{a}{a-1}+\dfrac{2a^2}{\left(a-1\right)\left(a+1\right)}\)
\(=\dfrac{a\left(a-1\right)-a\left(a+1\right)+2a^2}{\left(a+1\right)\left(a-1\right)}\)
\(=\dfrac{a^2-a-a^2-a+2a^2}{\left(a+1\right)\left(a-1\right)}=-\dfrac{2a}{a^2-1}\)
g: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
\(\dfrac{4}{x+2}+\dfrac{2}{x-2}+\dfrac{5x-6}{4-x^2}\)
\(=\dfrac{4}{x+2}+\dfrac{2}{x-2}-\dfrac{5x-6}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{4\left(x-2\right)+2\left(x+2\right)-5x+6}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{4x-8+2x+4-5x+6}{\left(x-2\right)\left(x+2\right)}=\dfrac{x+2}{\left(x-2\right)\left(x+2\right)}=\dfrac{1}{x-2}\)
h: ĐKXĐ: x<>1
\(\dfrac{x^2+2}{x^3-1}+\dfrac{2}{x^2+x+1}-\dfrac{1}{x-1}\)
\(=\dfrac{x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{2}{x^2+x+1}-\dfrac{1}{x-1}\)
\(=\dfrac{x^2+2+2\left(x-1\right)-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{-x+1+2x-2}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{1}{x^2+x+1}\)