Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Gọi x; y lần lượt là số xe loại M, loại F cần thuê
Từ bài toán ta được hệ bất phương trình
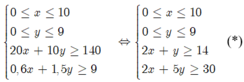
Tổng chi phí T(x; y) = 4x+ 3y (triệu đồng)
Bài toán trở thành là tìm x; y nguyên không âm thoả mãn hệ (*) sao cho T( ;xy) nhỏ nhất.
Từ đó ta cần thuê 5 xe hiệu M và 4 xe hiệu F thì chi phí vận tải là thấp nhất.

Doanh thu khi bán Q sản phẩm là 170Q nghìn đồng.
Lợi nhuận khi bán Q sản phẩm là \(170Q - \left( {{Q^2} + 30Q + 3300} \right)\)\( = - {Q^2} + 140Q - 3300\)(nghìn đồng)
Để không bị lỗ thì \( - {Q^2} + 140Q - 3300 \ge 0\left( 1 \right)\)
\(a = - 1 < 0;\Delta ' = 1600\)
\( - {Q^2} + 140Q - 3300 = 0\) có 2 nghiệm phân biệt \({x_1} = 30,{x_2} = 110\)
(1)\( \Leftrightarrow \)\(30 \le x \le 110\)
Vậy để không bị lỗ thì số sản phẩm được sản suất phải nằm trong khoảng từ 30 đến 110 sản phẩm.

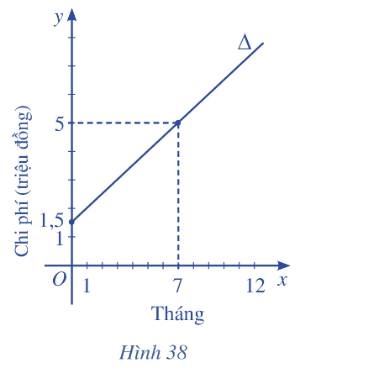
a) Đường thẳng \(\Delta \) đi qua hai điểm lần lượt có tọa độ \(\left( {0;1,5} \right),\left( {7;5} \right)\) nên \(\Delta \) có phương trình là:
\(\frac{{x - 0}}{{7 - 0}} = \frac{{y - 1,5}}{{5 - 1,5}} \Leftrightarrow \frac{x}{7} = \frac{{y - 1,5}}{{3,5}} \Leftrightarrow x - 2y + 3 = 0\)
b) Giao điểm của đường thẳng \(\Delta \) với trục \(Oy\) ứng với \(x = 0\). Thời điểm \(x = 0\)cho biết khoản phí tham gia ban đầu mà người tập phải trả. Khi \(x = 0\) thì \(y = 1,5\) , vì vậy khoản phí tham gia ban đầu mà người tập phải trả là 1 500 000 đồng.
c) 12 tháng đầu tiên ứng với \(x = 12\)
Từ phương trình đường thẳng \(\Delta \) ta có: \(x - 2y + 3 = 0 \Leftrightarrow y = \frac{1}{2}x + \frac{3}{2}\)
Thay \(x = 12\) vào phương trình đường thẳng ta có: \(y = \frac{1}{2}.12 + \frac{3}{2} = 7.5\)
Vậy tổng chi phí mà người đó phải trả khi tham gia phòng tập thể dục trong 12 tháng là 7tr5 nghìn đồng.