
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi x, y lần luợt là số lần phát quảng cáo vào khoảng 20h30 và vào khung giờ 16h00-17h00. \((x,y \in \mathbb{N})\)
Trong toán học, các điều kiện để đáp ứng nhu cầu trên của công ty đuợc thể hiện là:
+) ít nhất 10 lần quảng cáo vào khoảng 20h30: \(x \ge 10\)
+) không quá 50 lần quảng cáo vào khung giờ 16h00-17h00: \(y \le 50\)
+) chi không quá 900 triệu đồng: \(30.x + 6.y \le 900\)

Chọn C
+ Gọi thời lượng công ty đặt quảng cáo trên sóng phát thanh là x (phút), trên truyền hình là y (phút). Chi phí cho việc này là:800.000x + 4.000.000y (đồng)
Mức chi này không được phép vượt qúa mức chi tối đa, tức:
800.000x+ 4.000.000y ≤ 16.000.000 hay x+ 5y-20 ≤ 0
Do các điều kiện đài phát thanh, truyền hình đưa ra, ta có:x ≥ 5 và y ≤ 4
Đồng thời do x; y là thời lượng nên x; y ≥ 0
Hiệu quả chung của quảng cáo là x+ 6y.
Bài toán trở thành: Xác định x; y sao cho:
M( x; y) = x + 6y đạt giá trị lớn nhất.
Với các điều kiện : 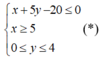
Trước tiên ta xác định miền nghiệm của hệ bất phương trình (*)
+Trong mặt phẳng tọa độ vẽ các đường thẳng
(d) : x + 5y - 20= 0 và (d’) ; x = 5; ( d’’) y = 4.
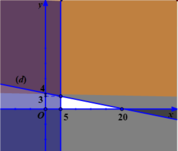
Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(tam giác) không tô màu trên hình vẽ
Giá trị lớn nhất của M( x; y) =x+ 6y đạt tại một trong các điểm (5;3) ; ( 5;0) và ( 20; 0).
Ta có M (5; 3) = 23; M( 5; 0) = 5 và M( 20; 0) = 20.
+ Suy ra giá trị lớn nhất của M( x; y) bằng 23 tại ( 5; 3) tức là nếu đặt thời lượng quảng cáo trên sóng phát thanh là 5 phút và trên truyền hình là 3 phút thì sẽ đạt hiệu quả nhất.

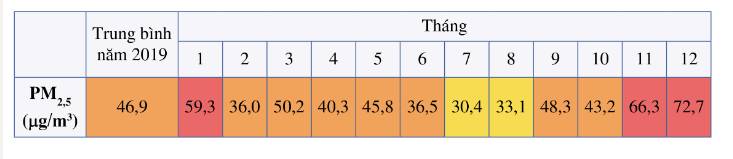
a) Từ bảng ta thấy:
Tháng 2: chỉ số \(P{M_{2,5}}\) là 36,0\(\left( {\mu g/{m^3}} \right)\)
Tháng 5: chỉ số \(P{M_{2,5}}\) là 45,8\(\left( {\mu g/{m^3}} \right)\)
Tháng 10: chỉ số \(P{M_{2,5}}\) là 43,2\(\left( {\mu g/{m^3}} \right)\)
b) Chỉ số \(P{M_{2,5}}\) là hàm số của tháng vì với mỗi tháng có đúng một chỉ số \(P{M_{2,5}}\) tương ứng.

Tham khảo:
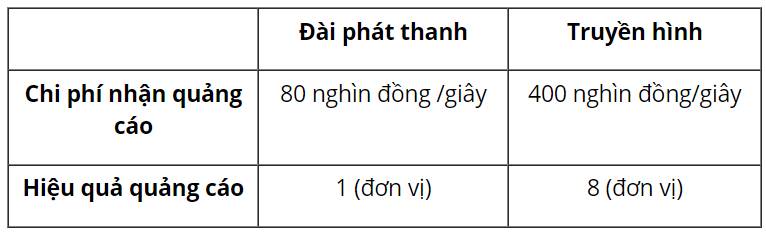
Gọi x và y là số giây quảng cáo trên đài phát thanh và trên truyền hình.
Khi đó \(x \ge 0;y \ge 0\)
160 triệu đồng=160000 (nghìn đồng)
Chi phí quảng cáo x giây trên đài phát thanh và y giây trên truyền hình là \(80x + 400y\)(nghìn đồng)
Vì công ty dự chi tối đa 160 triệu đồng nên ta có
\(80x + 400y \le 160000\)\( \Leftrightarrow x + 5y \le 2000\)
Đài phát thanh chỉ nhận các quảng cáo có tổng thời lượng trong một tháng tối đa là 900 giây nên ta có: \(x \le 900\)
Đài truyền hình chỉ nhận các quảng cáo có tổng thời lượng trong một tháng tối đa là 360 giây nên ta có: \(y \le 360\)
Ta có hệ bất phương trình:
\(\left\{ {\begin{array}{*{20}{l}}
{x \ge 0}\\
{y \ge 0}\\
{x + 5y \le 2000}\\
{x \le 900}\\
{y \le 360}
\end{array}} \right.\)
Xác định miền nghiệm là miền ngũ giác OABCD với:
A(900;0); B(900;220); C(200;360); D(0;360)
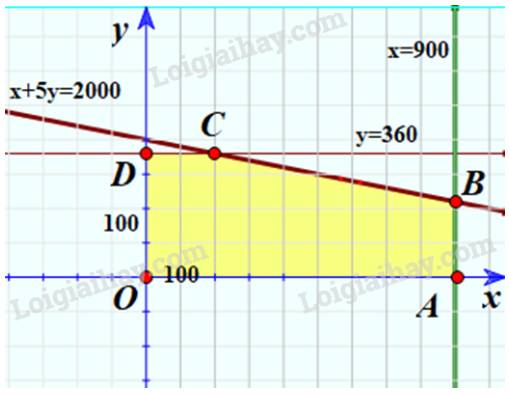
Hiệu quả quảng cáo là: \(F\left( {x;y} \right) = x + 8y\)
Ta có:
\(F\left( {0;0} \right) = 0\)
\(F\left( {900;0} \right) = 900 + 8.0 = 900\)
\(F\left( {900;220} \right) = 900 + 8.220 = 2660\)
\(F\left( {200;360} \right) = 3080\)
\(F\left( {0;360} \right) = 2880\)
Vậy công ty cần đặt thời gian quảng cáo trên đài phát thanh là 200 giây và trên truyền hình là 360 giây thì hiệu quả nhất.

Vì độ chính xác đến hàng trăm ( d = 150 ) nên ta quy tròn a đến hàng nghìn. Vậy số quy tròn của a là 1 718 000.
Đáp án là A.

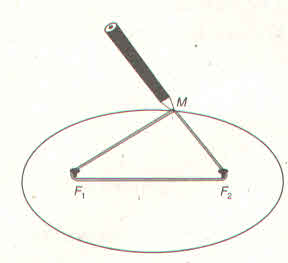
Ta có: 2a = 80 => a = 40
2b = 40 => b = 20
c2 = a2 – b2 = 1200 => c = 20√3
Phải đóng đinh tại các điểm F1 , F2 và cách mép ván:
F2A = OA – OF2 = 40 – 20√3
=> F2A = 20(2 – √3) ≈ 5,4cm
Chu vi vòng dây bằng: F1.F2+ 2a = 40√3 + 80
=> F1.F2 + 2a = 40(2 + √3)
F1.F2 + 2a ≈ 149,3cm

Ta có: 2a = 80 => a = 40
2b = 40 => b = 20
c2 = a2 – b2 = 1200 => c = 20√3
Phải đóng đinh tại các điểm F1 , F2 và cách mép ván:
F2A = OA – OF2 = 40 - 20√3
=> F2A = 20(2 - √3) ≈ 5,4cm
Chu vi vòng dây bằng: F1.F2+ 2a = 40√3 + 80
=> F1.F2 + 2a = 40(2 + √3)
F1.F2 + 2a ≈ 149,3cm
phần đổi hình nền khóa r
mk ko biết sory nha