Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số hạt nhân bị phân rã là DN=N0.2-t/T => số hạt Pononi còn lại là N=DN= N0.2-t/T
Mỗi hạt Pononi phân rã tạo thành 1 hạt nhân chì=>NPb=DN=N0.2-t/T
Tại thời điểm t1

Đáp án D

Cứ mỗi hạt nhân Pôlôni bị phân rã tạo thành 1 hạt nhân chì trong mẫu.
Số hạt nhân Pôlôni bị phân rã là \(\Delta N = N_0 2^{-\frac{t}{T}}.\)
Số hạt nhân Pônôni còn lại là \( N = N_0 2^{-\frac{t}{T}}.\)
Tại thời điểm t1 : \(\frac{\Delta N}{N } = \frac{1-2^{-\frac{t_1}{T}}}{2^{-\frac{t_1}{T}}}= \frac{1}{3}\)
=> \(3(1-2^{-\frac{t_1}{T}})= 2^{-\frac{t_1}{T}}\)
=> \(2^{-\frac{t_1}{T}}= 2^{-2}\)
=> \(t_1 = 2T\)
=> \(t_2 = 2T+276 = 552 \) (ngày)
=> \(\frac{t_2}{T}= \frac{552}{138}= 4.\)
Tại thời điểm t2 : \(\frac{\Delta N_1}{N_1 } = \frac{1-2^{-\frac{t_2}{T}}}{2^{-\frac{t_2}{T}}}= \frac{1-2^{-4}}{2^{-4}}= 15.\)
=> \(\frac{N_1}{\Delta N_1} = \frac{1}{15}.\)

Đáp án: C.
Tại thời điểm t1, NPo/NPb = NPo/(N0 – NPo) = 1/3 ⇒ NPo = N0/4 ⇒ t1 = 2T
Tại thời điểm t2 = t1 + 276= 2T + 2T = 4T
⇒ số hạt nhân Po còn lại NPo = N0/24 = N0/16 ⇒ NPb = 15N0/16 ⇒ NPo/NPb = 1/15.

- Tại thời điểm t1:
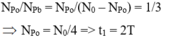
- Tại thời điểm t2 = t1 + 276= 2T + 2T = 4T.
→ Số hạt nhân Po còn lại:
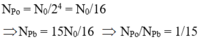

Tại thời điểm t1, NPo/NPb = NPo/(N0 – NPo) = 1/3
=> NPo = N0/4 => t1 = 2T
Tại thời điểm t2 = t1 + 276= 2T + 2T = 4T
=> số hạt nhân Po còn lại NPo = N0/24 = N0/16
=> NPb = 15N0/16 => NPo/NPb = 1/15
Chọn đáp án C


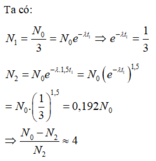

Đáp án C