Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi H là trực tâm tam giác ABC và O là giao 3 đường trung trực của tg ABC
=> O là tâm đường tròng ngoại tiếp tg ABC
Nối A với O kéo dài cắt (O) tại D
Xét tứ giác BHCD có
BH vuông góc AC
^ACD=90 (góc nt chắn nửa đường tròn)
=> CD vuông góc AC
=> BH//CD (BH, CD cùng vuông góc với AC) (1)
CH vuông góc AB
^ABD=90 (góc nt chắn nửa đường tròn)
=> BD vuông góc AB
=> CH//BD (CH, BD cùng vuông góc với AB) (2)
Từ (1) và (2) => BHCD là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau thì là hbh)
Gọi M là trung điểm BC => OM là đường trung trực của tg ABC thuộc cạnh BC => OM vuông góc với BC
AH vuông góc BC
=> AH//OM (cùng vuông góc với BC)
Xét hình bình hành BHCD
Do M là trung điểm của BC => M cũng là trung điểm của HD (trong hình bình hành hai đường chéo cắt nhau tại trung điểm mỗi đường)
=> Áp dụng talet trong tam giác \(\Rightarrow\frac{DM}{DH}=\frac{OM}{AH}=\frac{1}{2}\Rightarrow AH=2.OM\)

,2x^2-12x+18+2xy-6y
= 2(x^2-6x+9) + 2y(x-3)
= 2(x-3)^2 + 2y(x-3)
= (x-3)(2x-6+2y)

a,=(x\(^2\)-6x+9)+10-9
=(x-3)\(^2\)+1
Mà(x-3)\(^2\)\(\ge\)0
nên (x-3)\(^2\)+1>0
b,= -(-4x+x\(^2\))-5
= -(4-4x+x\(^2\))-5+4
= -(2-x)\(^2\)-1
Mà -(2-x)\(^2\)\(\le\)0
nên -(2-x)\(^2\)-1< 0
Võ Hoàng Tiên: Cảm ơn pạn nhiều lắm =)) nek :3 Hí Hí :) Thankssssss

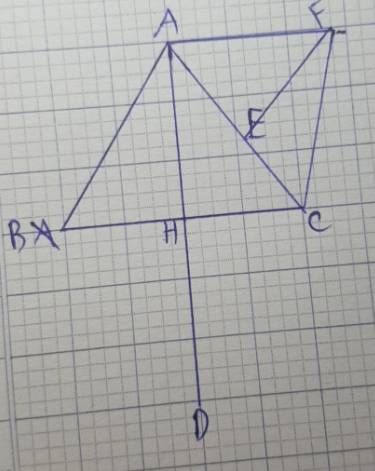
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
Xét tứ giác ABDC có
H là trung điểm chung của AD và BC
nên ABDC là hình bình hành
Hình bình hành ABDC có AB=AC
nên ABDC là hình thoi
b: H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=3\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=5^2-3^2=16\)
=>AH=4(cm)
AD=2*AH
=>AD=2*4=8(cm)
c:
Xét tứ giác AHCF có
E là trung điểm chung của AC và HF
nên AHCF là hình bình hành
Hình bình hành AHCF có \(\widehat{AHC}=90^0\)
nên AHCF là hình chữ nhật
=>AH\(\perp\)AF và HC\(\perp\)FC
d: ABDC là hình thoi
=>\(\widehat{BAC}=\widehat{BDC}=60^0\)
ABDC là hình thoi
=>\(\widehat{ABD}+\widehat{BAC}=180^0\)
=>\(\widehat{ABD}=120^0\)
ABDC là hình thoi
=>\(\widehat{ABD}=\widehat{ACD}=120^0\)


Đáp án :
7 - 1
= 6
Học tốt
7-1=6 (mk rất ghét BTS NAK BN)