Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Hàm có cực đại, cực tiểu khi mà $y'=-3x^2+2(m-1)x=x[2(m-1)-3x]$ có ít nhất hai nghiệm phân biệt $\Leftrightarrow 2(m-1)-3x=0$ có một nghiệm khác $0$ hay $m\neq 1$
b) Đồ thị hàm số $(\star)$ cắt trục hoành tại ba điểm phân biệt khi mà phương trình $y=-x^3+(m-1)x^2-m+2=0$ có $3$ nghiệm phân biệt
$\Leftrightarrow (1-x)[x^2+x(2-m)+(2-m)]=0$ có ba nghiệm phân biệt
$\Leftrightarrow x^2+x(2-m)+(2-m)=0$ có hai nghiệm phân biệt khác $1$
Do đó ta cần có $\left\{\begin{matrix}1+2-m+2-m=5-2m\neq 0\\ \Delta =(2-m)^2-4(2-m)>0\end{matrix}\right.$
Vậy để thỏa mãn đề bài thì $m\neq \frac{5}{2}$ và $m>2$ hoặc $m<-2$
c) Gọi điểm cố định mà đồ thị hàm số đi qua là $(x_0,y_0)$
$y_0=-x_0^3+(m-1)x_0^2-m+2$ $\forall m\in\mathbb{R}$
$\Leftrightarrow m(x_0^2-1)-(x_0^3+x_0^2+y_0-2)=0$ $\forall m\in\mathbb{R}$
$\Rightarrow\left{\begin{matrix}x_0^2=1\\ x_0^3+x_0^2+y_02=0\end{matrix}\right.\begin{bmatrix}(x_0,y_0)=(1;0)\\ (x_0,y_0)=(-1;2)\end{bmatrix}$
Viết lại đoạn cuối:
$\Rightarrow\left{\begin{matrix}x_0^2=1\\x_0^3+x_0^2+y_0-2=0\end{matrix}\right.$ $\Rightarrow \begin{bmatrix}(x_0,y_0)=(1;0)\\ (x_0,y_0)=(-1;2)\end{bmatrix}$

Giải:
a) Xét \(y'=3x^2+2mx\)
Ta thấy \(y'=3x^2+2mx=0\) có \(\Delta'=m^2>0\forall m\neq 0\) nên luôn có hai nghiệm phân biệt, đồng nghĩa với hàm số đã cho luôn có cực đại, cực tiểu với mọi \(m\neq 0\)
b) Đồ thị hàm số luôn cắt trục hoành tại điểm có hoành độ dương với mọi giá trị của $m$ nghĩa là phương trình \(x^3+mx^2-1=0\) luôn có nghiệm dương với mọi \(m\)
Xét hàm $y$ liên tục trên tập xác định.
Nếu \(m>0\) có \(\left\{\begin{matrix} f(0)=-1<0\\ f(m+1)=(m+1)^3+m(m+1)^2-1>0\end{matrix}\right.\Rightarrow f(0).f(m+1)<0\)
Do đó phương trình luôn có nghiệm thuộc khoảng \((0;m+1)\), tức là nghiệm dương.
Nếu \(m<0\) có \(\left\{\begin{matrix} f(0)=-1<0\\ f(1-m)=m^2-2m>0\forall m<0\end{matrix}\right.\Rightarrow f(0).f(1-m)<0\)
Do đó phương trình luôn có nghiệm thuộc khoảng \((0,1-m)\) , tức nghiệm dương
Từ hai TH ta có đpcm.
c) Để pt có $3$ nghiệm phân biệt thì \(y'=3x^2+2mx\) phải có hai nghiệm phân biệt \(x_1,x_2\) thỏa mãn \(f(x_1)f(x_2)<0\)
Kết hợp với định lý Viete:
\(\Leftrightarrow x_1^3+x_2^3+m(x_1^2+x_2^2)-1>0\)
\(\Leftrightarrow 4m^3-27>0\Leftrightarrow m>\frac{3}{\sqrt[3]{4}}\)

a) Xét hàm số \(y=ax^4+bx^2+c\)
Ta có \(y'=4ax^3+2bx=2x\left(2ax^2+b\right)\)
\(y'=0\Leftrightarrow x=0\) hoặc \(2ax^2+b=0\left(1\right)\)
Đồ thị hàm số có 3 cực trị phân biệt khi và chỉ khi \(y'=0\) có 3 nghiệm phân biệt hay phương trình (1) có 2 nghiệm phân biệt khác 0 \(\Leftrightarrow ab< 0\) (*)
Với điều kiện (*) thì đồ thị có 3 điểm cực trị là :
\(A\left(0;c\right);B\left(-\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right);C\left(\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right)\)
Ta có \(AB=AC=\sqrt{\frac{b^2-8ab}{16a^2}};BC=\sqrt{-\frac{2b}{a}}\) nên tam giác ABC vuông khi và chỉ khi vuông tại A.
Khi đó \(BC^2=2AB^2\Leftrightarrow b^3+8a=0\)
Do đó yêu cầu bài toán\(\Leftrightarrow\begin{cases}ab< 0\\b^3+8a=0\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\-8\left(m+1\right)^3+8=0\end{cases}\)\(\Leftrightarrow m=0\)
b) Ta có yêu cầu bài toán \(\Leftrightarrow\begin{cases}ab< 0\\OA=BC\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\m^2-4\left(m+1\right)=0\end{cases}\)
\(\Leftrightarrow m=2\pm2\sqrt{2}\)

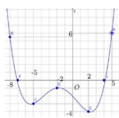
Ta có các điểm cực trị của (C) là A(0;4); B(2;0)
Gọi M (x;y) thuộc (P) : \(y=x^2\) khi đó \(\overrightarrow{MA}=\left(x;x^2-4\right);\overrightarrow{MB}=\left(x-2;\right)x^2\)
Tam giác AMB vuông tại M \(\Leftrightarrow\overrightarrow{AM}.\overrightarrow{BM}=0\Leftrightarrow x\left(x-2\right)+x^2\left(x^2-4\right)=0\)
\(\Leftrightarrow x\left(x^3-3x-2\right)=0\)
\(\Leftrightarrow x\left(x+1\right)^2\left(x-2\right)=0\)
Vậy có 3 điểm M thuộc (P) để tam giác AMB vuông tại M là \(M_1\left(0;0\right);M_2\left(-1;1\right);M_3\left(2;4\right)\)

Lần sau em đăng trong h.vn
1. \(log_{ab}c=\frac{1}{log_cab}=\frac{1}{log_ca+log_cb}=\frac{1}{\frac{1}{log_ac}+\frac{1}{log_bc}}=\frac{1}{\frac{log_ac+log_bc}{log_ac.log_bc}}=\frac{log_ac.log_bc}{log_ac+log_bc}\)
Đáp án B:
2. \(f'\left(x\right)=-4x^3+8x\)
\(f'\left(x\right)=0\Leftrightarrow-4x^3+8x=0\Leftrightarrow x=0,x=\sqrt{2},x=-\sqrt{2}\)
Có BBT:
x -căn2 0 căn2 f' f 0 0 0 - + - +
Nhìn vào bảng biên thiên ta có hàm số ... là đáp án C

Lời giải:
Vì hai điểm \((0,0);(1;1)\) thuộc đồ thị hàm số đã cho nên:
\(\left\{\begin{matrix} 0=a.0^3+b.0^2+c.0+d=d\\ 1=a+b+c+d\end{matrix}\right.(1)\)
Vì \((0,0);(1,1)\) là hai điểm cực trị nên \(0,1\) là hai nghiệm của PT :
\(y'=3ax^2+2bx+c=0\)
Do đó , áp dụng định lý Viete ta có:
\(\left\{\begin{matrix} 1+0=\frac{-2b}{3a}\\ 1.0=\frac{c}{3a}\end{matrix}\right.\Leftrightarrow \) \(\left\{\begin{matrix} 3a+2b=0\\ c=0\end {matrix}\right.(2)\)
Từ \((1),(2)\) giải hệ pt thu được \(\left\{\begin{matrix} a=-2\\ b=3\\ c=0\\ d=0\end{matrix}\right.\)

Chọn C.
![]()
![]()
Đồ thị hàm số có 3 điểm cực trị ⇔ m > 0
Khi đó, tọa độ ba điểm cực trị là
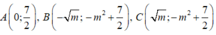
O là trực tâm tam giác
![]()

![]()
![]()
![]()
![]()
Vậy, chọn phương án C.


\(y'=3x^2+2bx+c\)
Gọi \(x_1\) và \(x_2\) là 2 nghiệm của pt \(3x^2+2bx+c=0\)
\(\Rightarrow x_1+x_2=-\frac{2b}{3}\) ; \(x_1x_2=\frac{c}{3}\)
Mà I là trung điểm 2 cực trị \(\Rightarrow x_1+x_2=2x_I=4\)
\(\Rightarrow-\frac{2b}{3}=4\Rightarrow b=-6\)
Mặt khác \(y_1+y_2=2y_I=4\)
\(\Rightarrow x_1^3+x_2^3-6\left(x_1^2+x_2^2\right)+c\left(x_1+x_2\right)+6=4\)
\(\Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)-6\left(x_1+x_2\right)^2+12x_1x_2+c\left(x_1+x_2\right)+2=0\)
\(\Leftrightarrow4^3-3.\frac{c}{3}.4-6.4^2+12.\frac{c}{3}+c.4+2=0\)
\(\Leftrightarrow4c=30\Rightarrow c=\frac{15}{2}\)
\(\Rightarrow\) Không có kết quả nào đúng
Đã kiểm tra lại kết quả bằng casio, ko thể sai được, cho nên hoặc là bạn ghi nhầm đề ở đâu đó, hoặc là các đáp án sai.
Vâng. Em cảm ơn ạ.