Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có M và N là hai điểm trên mặt nước và cùng cách đều A,B những đoạn là 16 cm nên M và N đều thuộc đường trung trực của AB và M N đối xứng nhau qua AB
như vậy trên đoạn OM có 3 điểm dao động cùng pha với nguồn
Do N đối xứng với M qua O nên trên đoạn ON cũng có 3 điểm dao động cùng pha với nguồn
Do trên đoạn ON và OM trùng nhau vân tại O nên trên đoạn MN có 5 điểm dao động cùng pha với nguồn

+ Hai điểm M, N nằm trên cùng một phương truyền sóng dao động ngược pha nhau:
∆ φ = 2 π x λ = ( 2 k + 1 ) ⇔ 2 π f x v = ( 2 k + 1 ) π
⇒ f = ( 2 k + 1 ) v 2 x = 8 ( 2 k + 1 )
+ Với khoảng cách giá trị của f: 48 ≤ f ≤ 64
Sử dụng Mode → 7 ta tìm được f = 56 Hz
Chọn A

Đáp án B
HD: + Độ lệch pha giữa hai điểm M, N:

+ Với khoảng giá trị của tốc độ truyền sóng 70cm/s ≤ v ≤ 80 c m / s . Kết hợp với chức năng Mode → 7, ta tìm được v = 75 cm/s

Đáp án C
+ Độ lệch pha giữa hai điểm M và N:
∆ φ = 2 πdf v = ( 2 k + 1 ) π → f = ( 2 k + 1 ) v 2 d = 8 ( 2 k + 1 ) Hz
+ Với khoảng giá trị của tần số:
48 Hz ≤ f ≤ 64 Hz → f = 56 Hz .

Đáp án B
+ Độ lệch pha giữa hai điểm A và B:
∆ φ A B = 2 π ∆ x A B f v = ( 2 k + 1 ) π → v = 4 2 k + 1 m/s
+ Với khoảng giả trị của vận tốc: 0 , 7 m / s ≤ v ≤ 1 m / s → v = 0 , 8 m → λ = 4 cm

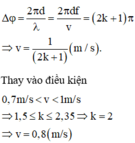

Hai điểm A và B dao động ngược pha nhau.
\(x_A-x_B=\left(2k+1\right)\dfrac{\lambda}{2}\)
\(\Rightarrow d=AB=\left(k+0,5\right)\cdot\dfrac{v}{f}\)
\(\Rightarrow v=\dfrac{f\cdot d}{k+0,5}=\dfrac{40\cdot0,2}{k+0,5}=\dfrac{8}{k+0,5}\)
Mà \(3\le v\le5\Rightarrow3\le\dfrac{8}{k+0,5}\le5\)
\(\Rightarrow1,1\le k\le2,17\), \(k\in Z\)\(\Rightarrow k=2\)
Vậy tốc độ truyền sóng:
\(v=\dfrac{8}{2+0,5}=\dfrac{8}{2,5}=3,2m/s\)