Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c: Theo câu b, ta được: H là tâm đường tròn ngoại tiếp ngũ giác DEKFO
OH vuông góc MN
=>MN là đường kính của (H)
=>HM=HN

B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)

a: Xéttứ giác AEHF có góc AEH+góc AFH=180 độ
nên AEHF là tứ giác nội tiếp
c: Xét tứ giác AEDC có góc ADC=góc AEC=90 độ
nên AEDC là tứ giác nội tiếp
d: góc EDA=góc ABF
góc FDA=góc FDH=góc ACE
mà góc ABF=góc ACE
nên góc EDA=góc FDA
=>DA là phân giác của góc EDF

cho tam giác ABC vuông cân tại B.Trên cạnh BA và BC lấy hai điểm E và F sao cho BE = BF.Qua B và E kẻ đường vuông góc với AF,chúng cắt AC lần lượt ở I và K. EK cắt BC tại H
a)Chứng minh tam giác AHC cân
b)chứng minh I là trung điểm KC
c)Gọi M,N,P lần lượt là trung điểm EC,AF,EF
Sửa đề: Đường tròn đường kính BC cắt AB, AC tại E và F
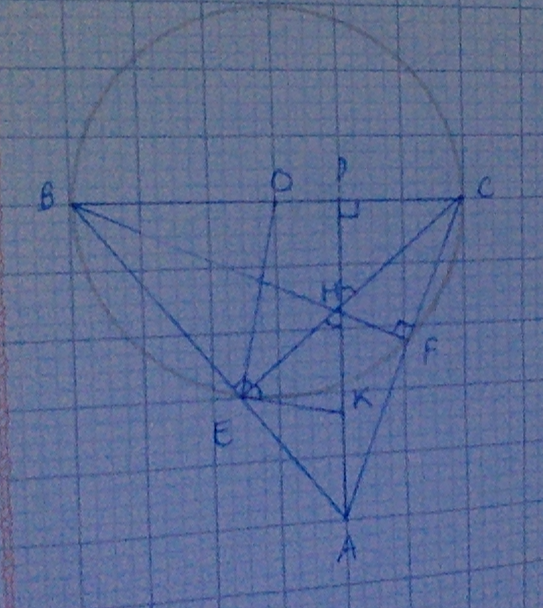
a) (O) có \(\widehat{BEC},\widehat{BFC}\) là 2 góc nội tiếp chắn nửa đường tròn nên \(\widehat{BEC}=90^o,\widehat{BFC}=90^o\Rightarrow CE\perp AB,BF\perp AC\). CE cắt BF tại H nên H là trực tâm của \(\Delta ABC\) => AH là đường cao thứ 3 => \(AH\perp BC\)
\(\widehat{BEC}=90^o\Rightarrow\widehat{AEH}=90^o.\widehat{BFC}=90^o\Rightarrow\widehat{AFH}=90^o\)
Tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=90^o+90^o=180^o\) nên nội tiếp.
Đường tròn ngoại tiếp tứ giác AEHF là đtron ngoại tiếp \(\Delta AEH\). \(\Delta AEH\) vuông tại E (\(\widehat{AEH}=90^o\)) nên tâm K của đường tròn này là trung điểm AH.
b) \(\Delta AEH\) vuông tại E có EK là trung tuyến (K là trđ AH) nên EK = AH/2 = KH = KA.
EK = KH nên \(\Delta EKH\) cân tại K => \(\widehat{KEH}=\widehat{KHE}\). Mà \(\widehat{KHE}=\widehat{DHC}\) (đối đỉnh) nên \(\widehat{KEH}=\widehat{DHC}\) (1)
\(\Delta OEC\) cân tại O (OE = OC = R) nên \(\widehat{OEC}=\widehat{OCE}=\widehat{HCD}\) (2)
\(\Delta DHC\) vuông tại D (\(AH\perp BC\)) nên \(\widehat{DHC}+\widehat{HCD}=90^o\) (3)
Từ (1), (2), (3) => \(\widehat{KEH}+\widehat{OEC}=90^o\Rightarrow\widehat{OEK}=90^o\Rightarrow OE\perp EK\). Lại có \(E\in\left(O\right)\) nên EK là tiếp tuyến của (O).