Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

mk nhầm câu c là 25f(x)
câu d là 24f(x)
mk nhầm nũa câu hỏi là cái f(x+2)-f(x) là bỏ nha

Lời giải:
Đặt \(\log_yx=a,\log_xy=b\). Khi đó ta có:
\(\left\{\begin{matrix} a+b=\frac{10}{3}\\ ab=\log_xy.\log_yx=1\end{matrix}\right.\)
Áp dụng định lý Viete đảo thì \(a,b\) là nghiệm của PT:
\(x^2-\frac{10}{3}x+1=0\) . PT trên có hai nghiệm \(3,\frac{1}{3}\)
Giả sử \(a=\log_yx=3\) và \(b=\log_xy=\frac{1}{3}\)
\(\left\{\begin{matrix} \log_y\left(\frac{144}{y}\right)=3\\ \log_x\left(\frac{144}{x}\right)=\frac{1}{3} \end{matrix}\right.\Rightarrow \left\{\begin{matrix} x=24\sqrt{3}\\ y=2\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow \frac{x+y}{2}=13\sqrt{3}\). Đáp án D

*Đặt tên các biểu thức theo thứ tự lần lượt là A,B,C,D,E,F *
Câu 1)
Ta có: \(d(\cos x)=(\cos x)'d(x)=-\sin xdx\)
\(\Rightarrow -d(\cos x)=\sin xdx\)
\(\Rightarrow A=\int \sqrt{3\cos x+2}\sin xdx=-\int \sqrt{3\cos x+2}d(\cos x)\)
Đặt \(\sqrt{3\cos x+2}=t\Rightarrow \cos x=\frac{t^2-2}{3}\)
\(\Rightarrow A=-\int td\left(\frac{t^2-2}{3}\right)=-\int t.\frac{2}{3}tdt=-\frac{2}{3}\int t^2dt=-\frac{2}{3}.\frac{t^3}{3}+c\)
\(=-\frac{2}{9}t^3+c=\frac{-2}{9}\sqrt{(3\cos x+2)^3}+c\)
Câu 2:
\(B=\int (1+\sin^3x)\cos xdx=\int \cos xdx+\int \sin ^3xcos xdx\)
\(=\int \cos xdx+\int \sin ^3xd(\sin x)\)
\(=\sin x+\frac{\sin ^4x}{4}+c\)
Câu 3:
\(C=\int \frac{e^x}{\sqrt{e^x-5}}dx=\int \frac{d(e^x)}{\sqrt{e^x-5}}\)
Đặt \(\sqrt{e^x-5}=t\Rightarrow e^x=t^2+5\)
Khi đó: \(C=\int \frac{d(t^2+5)}{t}=\int \frac{2tdt}{t}=\int 2dt=2t+c=2\sqrt{e^x-5}+c\)

a) Xét hàm số y = f(x) = tanx – x với x ∈ [0 ; ).
Ta có : y’ = - 1 ≥ 0, x ∈ [0 ;
); y’ = 0 ⇔ x = 0. Vậy hàm số luôn đồng biến trên [0 ;
).
Từ đó ∀x ∈ (0 ; ) thì f(x) > f(0) ⇔ tanx – x > tan0 – 0 = 0 hay tanx > x.
b) Xét hàm số y = g(x) = tanx – x - . với x ∈ [0 ;
).
Ta có : y’ = - 1 - x2 = 1 + tan2x - 1 - x2 = tan2x - x2
= (tanx - x)(tanx + x), ∀x ∈ [0 ; ).
Vì ∀x ∈ [0 ; ) nên tanx + x ≥ 0 và tanx - x >0 (theo câu a).
Do đó y' ≥ 0, ∀x ∈ [0 ; ).
Dễ thấy y' = 0 ⇔ x = 0. Vậy hàm số luôn đồng biến trên [0 ; ). Từ đó : ∀x ∈ [0 ;
) thì g(x) > g(0) ⇔ tanx – x -
> tan0 - 0 - 0 = 0 hay tanx > x +
.

Câu a: Tích phân không thể tính được
Câu b:
Đặt \(\sqrt{x}=t\). Khi đó:
\(\int ^{\pi ^2}_{0}x\sin \sqrt{x}dx=\int ^{\pi}_{0}t^2\sin td(t^2)\) \(=2\int ^{\pi}_{0}t^3\sin tdt\)
Tính \(\int t^3\sin tdt\) bằng nguyên hàm từng phần:
\(\Rightarrow \int t^3\sin tdt=\int t^3d(-\cos t)=-t^3\cos t+\int \cos t d(t^3)\)
\(=-t^3\cos t+3\int t^2\cos tdt\)
\(=-t^3\cos t+3\int t^2d(\sin t)=-t^3\cos t+3(t^2\sin t-\int \sin td(t^2))\)
\(=-t^3\cos t+3(t^2\sin t-2\int t\sin tdt)\)
\(=-t^3\cos t+3(t^2\sin t-2\int td(-cos t))\)
\(=-t^3\cos t+3[t^2\sin t-2(-t\cos t+\int \cos tdt)]\)
\(=-t^3\cos t+3t^2\sin t+6t\cos t-6\sin t+c\)
\(\Rightarrow 2\int ^{\pi}_{0}t^3\sin tdt=2(-t^3\cos t+3t^2\sin t+6t\cos t-6\sin t+c)\left|\begin{matrix} \pi\\ 0\end{matrix}\right.\)
\(=2\pi ^3-12\pi \)
Lời giải:
Đặt \(2x+1=t\Rightarrow x=\frac{t-1}{2}\)
Khi đó:
\(\int ^{\frac{1}{9}}_{0}\frac{x}{\sin ^2(2x+1)}dx=\frac{1}{2}\int ^{\frac{11}{9}}_{0}\frac{t-1}{\sin ^2t}d(\frac{t-1}{2})=\frac{1}{4}\int ^{\frac{11}{9}}_{1}\frac{t-1}{\sin ^2t}dt\)
Xét \(\int \frac{t-1}{\sin ^2t}dt=\int \frac{t}{\sin ^2t}dt-\int \frac{dt}{\sin ^2t}=\int td(-\cot t)-(-\cot t)+c\)
\(=(-t\cot t+\int \cot tdt)+\cot t+c\)
\(=-t\cot t+\int \frac{\cos t}{\sin t}dt+\cot t+c\)
\(=-t\cot t+\int \frac{d(\sin t)}{\sin t}+\cot t+c\)
\(=-t\cot t+\ln |\sin t|+\cot t+c\)
\(\Rightarrow \frac{1}{4}\int ^{\frac{11}{9}}_{1}\frac{t-1}{\sin ^2t}dt=\frac{1}{4}(-t\cot t+\ln |\sin t|+\cot t+c)\left|\begin{matrix} \frac{11}{9}\\ 1\end{matrix}\right.\)
\(\approx 0,007\)

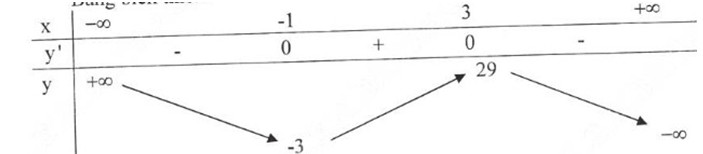
a) Tập xác định : D = R
limx→−∞f(x)=+∞limx→+∞f(x)=−∞y′=−3x2+6x+9=0⇔x=−1,x=3limx→−∞f(x)=+∞limx→+∞f(x)=−∞y′=−3x2+6x+9=0⇔x=−1,x=3
Bảng biến thiên:
Đồ thị hàm số:
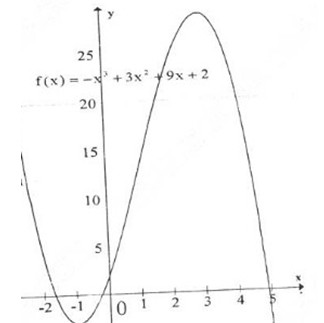
b) y=f(x) = f(x) = -x3+3x2+9x+2.
f’(x) = -3x2+6x+9. Do đó:
f’(x-1)=-3(x-1)2+6(x-1)+9
= -3x2 + 12x = -3x(x-4) > 0 ⇔ 0 < x < 4
c) f’’(x) = -6x+6
f’’(x0) = -6 ⇔ -6x0 + 6 = -6 ⇔ x0 = 2
Do đó: f’(2) = 9, f(2) = 24. Phương trình tiếp tuyến của (C) tại x0 = 2 là:
y=f’(2)(x-2) + f(2) hay y = 9x+6

a)
Đặt \(\frac{x}{2}=t\Rightarrow 3^{2t}-4=5^t\)
\(\Leftrightarrow 9^t-5^t=4\)
TH1: \(t>1\Rightarrow 9^t-5^t< 4^t\)
\(\Leftrightarrow 9^t< 4^t+5^t\)
\(\Leftrightarrow 1< \left(\frac{4}{9}\right)^t+\left(\frac{5}{9}\right)^t\) \((*)\)
Ta thấy vì \(\frac{4}{9};\frac{5}{9}<1 \), do đó với \(t>1\Rightarrow \left\{\begin{matrix} \left(\frac{4}{9}\right)^t< \frac{4}{9}\\ \left(\frac{5}{9}\right)^t< \frac{5}{9}\end{matrix}\right.\)
\(\Rightarrow \left(\frac{4}{9}\right)^t+\left(\frac{5}{9}\right)^t< \frac{4}{9}+\frac{5}{9}=1\) (mâu thuẫn với (*))
TH2: \(t<1 \) tương tự TH1 ta cũng suy ra mâu thuẫn
do đó \(t=1\Rightarrow x=2\)
b)
Ta có: \(5^{2x}=3^{2x}+2.5^x+2.3^x\)
\(\Leftrightarrow (5^{2x}-2.5^{x}+1)=3^{2x}+2.3^x+1\)
\(\Leftrightarrow (5^x-1)^2=(3^x+1)^2\)
\(\Leftrightarrow (5^x-3^x-2)(5^x+3^x)=0\)
Dễ thấy \(5^x+3^x>0\forall x\in\mathbb{R}\Rightarrow 5^x-3^x-2=0\)
\(\Leftrightarrow 5^x-3^x=2\)
\(\Leftrightarrow 5^x=3^x+2\)
Đến đây ta đưa về dạng giống hệt phần a, ta thu được nghiệm \(x=1\)
c)
\((2-\sqrt{3})^x+(2+\sqrt{3})^x=4^x\)
\(\Leftrightarrow \left(\frac{2-\sqrt{3}}{4}\right)^x+\left(\frac{2+\sqrt{3}}{4}\right)^x=1\)
TH1: \(x>1\)
Vì \(\frac{2+\sqrt{3}}{4};\frac{2-\sqrt{3}}{4}<1;x> 1 \Rightarrow \left ( \frac{2-\sqrt{3}}{4} \right )^x< \frac{2-\sqrt{3}}{4};\left ( \frac{2+\sqrt{3}}{4} \right )^x< \frac{2+\sqrt{3}}{4}\)
\(\Rightarrow \left ( \frac{2-\sqrt{3}}{4} \right )^x+\left ( \frac{2+\sqrt{3}}{4} \right )^x<\frac{2-\sqrt{3}}{4}+\frac{2+\sqrt{3}}{4}=1\) (vô lý)
TH2: \(x<1 \)
\(\frac{2+\sqrt{3}}{4};\frac{2-\sqrt{3}}{4}<1; x< 1 \Rightarrow \left ( \frac{2-\sqrt{3}}{4} \right )^x> \frac{2-\sqrt{3}}{4};\left ( \frac{2+\sqrt{3}}{4} \right )^x> \frac{2+\sqrt{3}}{4}\)
\(\Rightarrow \left ( \frac{2-\sqrt{3}}{4} \right )^x+\left ( \frac{2+\sqrt{3}}{4} \right )^x>\frac{2-\sqrt{3}}{4}+\frac{2+\sqrt{3}}{4}=1\) (vô lý)
Do đó \(x=1\)

\(\int\left(\frac{1}{x}-2x\right)dx=ln\left|x\right|-x^2+C\)
\(\int cos2xdx=\frac{1}{2}sin2x+C\)
\(\int\frac{1}{x^2-4x+4}dx=\int\frac{d\left(x-2\right)}{\left(x-2\right)^2}=-\frac{1}{\left(x-2\right)}+C=\frac{1}{2-x}+C\)
\(\int\limits^4_1\frac{1}{2\sqrt{x}}dx=\sqrt{x}|^4_1=\sqrt{4}-\sqrt{1}=1\)
\(I=\int\limits^1_0\left(2x+1\right)e^xdx\)
Đặt \(\left\{{}\begin{matrix}u=2x+1\\dv=e^xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2dx\\v=e^x\end{matrix}\right.\)
\(\Rightarrow I=\left(2x+1\right)e^x|^1_0-\int\limits^1_02e^xdx=3e-1-2e^x|^1_0=e+3\)