Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y=\dfrac{x+2}{x+1}\Rightarrow y'=\dfrac{-1}{\left(x+1\right)^2}\)
Gọi giao điểm của tiếp tuyến tại M với 2 trục lần lượt là A và B
Do tam giác OAB vuông cân \(\Rightarrow\widehat{ABO}=45^0\)
\(\Rightarrow\) Tiếp tuyến tạo với trục hoành một góc \(45^0\) hoặc \(135^0\)
\(\Rightarrow\) Hệ số góc k của tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}k=tan45^0=1\\k=tan135^0=-1\end{matrix}\right.\)
Gọi \(M\left(x_0;y_0\right)\) \(\Rightarrow y'\left(x_0\right)=k\Rightarrow\left[{}\begin{matrix}\dfrac{-1}{\left(x_0+1\right)^2}=1\left(vô-nghiệm\right)\\\dfrac{-1}{\left(x_0+1\right)^2}=-1\end{matrix}\right.\)
\(\Rightarrow\left(x_0+1\right)^2=1\Rightarrow\left[{}\begin{matrix}x_0=0\Rightarrow y_0=2\\x_0=-2\Rightarrow y_0=0\end{matrix}\right.\)
Có 2 điểm M thỏa mãn: \(\left[{}\begin{matrix}M\left(0;2\right)\\M\left(-2;0\right)\end{matrix}\right.\)

Xét phương trình tiếp tuyến tổng quát có dạng:
\(y=\left(6x_0+3x_0^2\right)\left(x-x_0\right)+3x_0^2+x_0^3\)
có 3 tiếp tuyến đi qua A(a,0) nên phương trình \(\left(6x_0+3x_0^2\right)\left(a-x_0\right)+3x_0^2+x_0^3=0\) có 3 nghiệm
\(PT\Leftrightarrow\orbr{\begin{cases}x_0=0\\2x_0^2+3\left(1-a\right)x_0+6a=0\end{cases}}\)
Vậy có 1 pttt là y=0
do đó để có hai tiếp tuyến vuông góc thì \(2x_0^2+3\left(1-a\right)x_0+6a=0\) có hia nghiệm \(x_1,x_2\text{ thỏa mãn}\)
\(\left(6x_1+3x_1^2\right)\left(6x_2+3x_2^2\right)=-1\)mà áp dung Viet ta có \(\hept{\begin{cases}x_1+x_2=\frac{3a-3}{2}\\x_1x_2=3a\end{cases}}\)
Nên \(36x_1x_2+18x_1x_2\left(x_1+x_2\right)+9x_1^2x_2^2=-1\Leftrightarrow126a+81a\left(a-1\right)+81a^2=-1\)
từ đây mình giải được a nhé
Xét phương trình tiếp tuyến tổng quát có dạng:
y=(6x0+3x02)(x−x0)+3x02+x03
có 3 tiếp tuyến đi qua A(a,0) nên phương trình (6x0+3x02)(a−x0)+3x02+x03=0 có 3 nghiệm
PT⇔[
| x0=0 |
| 2x02+3(1−a)x0+6a=0 |
Vậy có 1 pttt là y=0
do đó để có hai tiếp tuyến vuông góc thì 2x02+3(1−a)x0+6a=0 có hia nghiệm x1,x2 thỏa mãn
(6x1+3x12)(6x2+3x22)=−1mà áp dung Viet ta có {
| x1+x2=3a−32 |
| x1x2=3a |
Nên 36x1x2+18x1x2(x1+x2)+9x12x22=−1⇔126a+81a(a−1)+81a2=−1

- Hàm số đã cho xác định với ∀x ≠ 1.
- Ta có:
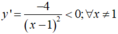
- Gọi M ( x 0 ; y 0 ) là tọa độ tiếp điểm, suy ra phương trình tiếp tuyến của (C):
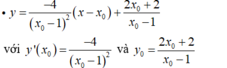
- Tiếp tuyến tạo với 2 trục tọa độ lập thành một tam giác cân nên hệ số góc của tiếp tuyến bằng ± 1. Mặt khác: y ' ( x 0 ) < 0 , nên có: y ' ( x 0 ) = - 1 .
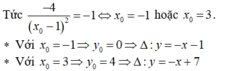
- Vậy, có 2 tiếp tuyến thỏa mãn đề bài: y = -x - 1; y = -x + 7.
Chọn D

\(y'=\dfrac{-4}{\left(x-1\right)^2}\)
a) \(y'=-1\Rightarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)
pt tiếp tuyến : \(\left[{}\begin{matrix}y=-\left(x-3\right)+4=-x+7\\y=-\left(x+1\right)=-x-1\end{matrix}\right.\)
b) \(k=\pm1\)
\(y'< 0\forall x\Rightarrow y'=-1\)
làm như trên
c) hoành độ tiếp điểm \(x=\pm2\)
TH x = 2
\(k=-4\)
pt tiếp tuyến : \(y=-4\left(x-2\right)+6=-4x+14\)
TH x = -2
\(k=-\dfrac{4}{9}\)
pt tiếp tuyến : \(y=-\dfrac{4}{9}\left(x+2\right)+\dfrac{2}{3}=-\dfrac{4}{9}x-\dfrac{2}{9}\)

Ta có: 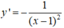
- Lấy điểm M(x0;y0) ∈ (C).
- Phương trình tiếp tuyến tại điểm M là:
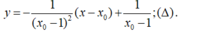
+ Giao với trục hoành: 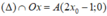
+ Giao với trục tung: 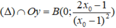
- Ta có:
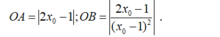
- Theo giả thiết tam giác OAB có diện tích bằng 2 nên:
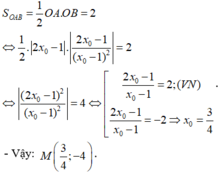

x^2+(y-1)^2=4
=>R=2 và I(0;1)
A(1;1-m) thuộc (C)
y'=4x^3-4mx
=>y'(1)=4-4m
PT Δsẽ là y=(4-m)(x-1)+1-m
Δ luôn đi qua F(3/4;0) và điểm F nằm trong (λ)
Giả sử (Δ) cắt (λ) tại M,N
\(MN=2\sqrt{R^2-d^2\left(I;\Delta\right)}=2\sqrt{4-d^2\left(I;\Delta\right)}\)
MN min khi d(I;(Δ)) max
=>d(I;(Δ))=IF
=>Δ vuông góc IF
Khi đó, Δ có 1 vecto chỉ phương là: vecto u vuông góc với vecto IF=(3/4;p-1)
=>vecto u=(1;4-4m)
=>1*3/4-(4-4m)=0
=>m=13/16

