KN
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MV
11 tháng 8 2017
Dãy này có quy luật: \(u_n=11n+1\)
a, Ta có: \(2012=2011+1\) mà \(2011⋮̸11\) nên \(2012\) không thuộc dãy số trên
b,
\(u_{2012}=11\cdot2012+1=22133\)
11 tháng 8 2017
a) ta có : dãy số sau có qui luật là (số sau) = (số trước) + 11
mà số đâu tiên là 12 \(\Rightarrow\) muôn biết 2012 có thuộc dãy số trên không thì đem 2012 trừ 12 rồi chia cho 11 (nêu ra số nguyên thì thuộc mà không nguyên thì không thuộc)
ta có : \(\dfrac{2012-12}{11}=\dfrac{2000}{11}\) (không nguyên) \(\Rightarrow\) 2012 không thuộc dãy số trên
b) số hạng thứ 2012 của dãy số trên là \(12+2012.11=12+22132=22144\)
vậy số hạng thứ 2012 của dãy số trên là \(22144\)
13 tháng 12 2015
a) Khong gian mau laf (a, b) voi a, b la so cham xuat hien o lan thu nhat va lan thu hai, a, b thuoc {1, 2, 3, 4 ,5 , 6}
b) - Xac suat lan dau xuat hien mat 5 cham la 1/6
- Xac suat de tong so cham cua hai lan gieo bang tong cac xac suat sau: (6,1) + (5,2) + (4,3) + (3,4) + (2,6) + (1,6) = 1/36 + 1/36 + 1/36 + 1/36 + 1/36 + 1/36 = 1/6
N
1
CM
26 tháng 4 2018
Chọn C
1. u n = 3 n + 1 2. u n = 4 − 5 n
3. u n = 2 n + 3 5 4. u n = n + 1 n
* Xét dãy số: u n = 3 n + 1
Ta có:
u n + 1 − u n = 3 ( n + 1 ) + 1 − 3 n − 1 = 3
Dãy số này là cấp số cộng có công sai d= 3.
* Xét dãy số u n = 4 − 5 n .
Ta có:
u n + 1 − u n = 4 − 5 ( n + 1 ) − ( 4 − 5 n ) = − 5
Dãy số này là cấp số cộng có công sai d = -5
* Xét dãy số u n = 2 n + 3 5
Ta có:
u n + 1 − u n = 2 ( n + 1 ) + 3 5 − 2 n + 3 5 = 2 5 .
Dãy (un) là cấp số cộng có công sai d = 2 5
* Xét dãy số u n = n + 1 n
Ta có:
u n + 1 − u n = n + 1 + 1 n + 1 − n + 1 n = ( n + 2 ) . n − ( n + 1 ) 2 n . ( n + 1 ) = − 1 n ( n + 1 ) ⇒ ( u n )
không là cấp số cộng
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 3 2020
1. Bạn ghi lại đề, mẫu số ko rõ
2. \(=lim\left[-8n^6\left(1-\frac{4}{n^2}\right)^3\right]=-\infty.1=-\infty\)
3. Dãy số là CSC với \(\left\{{}\begin{matrix}u_1=-1\\d=3\end{matrix}\right.\) \(\Rightarrow u_n=-1+\left(n-1\right)3=3n-4\)
\(\Rightarrow lim\frac{3n-4}{5n+2020}=lim\frac{3-\frac{4}{n}}{5+\frac{2020}{n}}=\frac{3}{5}\)
4.
\(u_{n+1}=\frac{1}{2}u_n+\frac{3}{2}\Rightarrow u_{n+1}-3=\frac{1}{2}\left(u_n-3\right)\)
Đặt \(v_n=u_n-3\Rightarrow\left\{{}\begin{matrix}v_1=-2\\v_{n+1}=\frac{1}{2}v_n\end{matrix}\right.\)
\(\Rightarrow v_n\) là CSN với công bội \(\frac{1}{2}\Rightarrow v_n=-2.\frac{1}{2^{n-1}}\Rightarrow u_n=v_n+3=-\frac{1}{2^{n-2}}+3\)
\(\Rightarrow lim\left(u_n\right)=lim\left[-\frac{1}{2^{n-2}}+3\right]=3\)
5.
\(u_{n+1}=u_n+\frac{1}{2^n}\Rightarrow u_{n+1}+\frac{2}{2^{n+1}}=u_n+\frac{2}{2^n}\)
Đặt \(v_n=u_n+\frac{2}{2^n}\Rightarrow\left\{{}\begin{matrix}v_1=3\\v_{n+1}=v_n\end{matrix}\right.\)
\(\Rightarrow v_{n+1}=v_n=...=v_1=3\Rightarrow u_n=3-\frac{2}{2^n}\)
\(\Rightarrow u_{n-2}=3-\frac{2}{2^{n-2}}\Rightarrow lim\left(u_{n-2}\right)=lim\left(3-\frac{2}{2^{n-2}}\right)=3\)
Tính \(u_{n-2}\) hay \(u_n-2\) nhỉ? Ko dịch nổi nên đoán đại
NH
1
15 tháng 10 2023
a: \(2n^2-3>=-3\)
\(\Leftrightarrow u_n=\dfrac{1}{2n^2-3}< =-\dfrac{1}{3}\)
=>Dãy số bị chặn trên ở -1/3
b: \(2n^2-1>=-1\)
=>\(u_n=\dfrac{1}{2n^2-1}< =\dfrac{1}{-1}=-1\)
=>Dãy số bị chặn trên ở -1
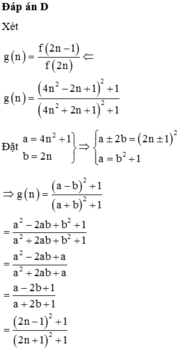
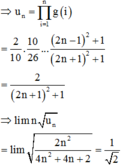
U1 = 2.1 - 1 = 1
U2 = 2.2 - 1 = 3
U3 = 2.3 - 1 = 5
U4 = 2.4 - 1 = 7
U5 = 2.5 - 1 = 9
U1=1
U2=3
U3=5
U4=7
U5=9