Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

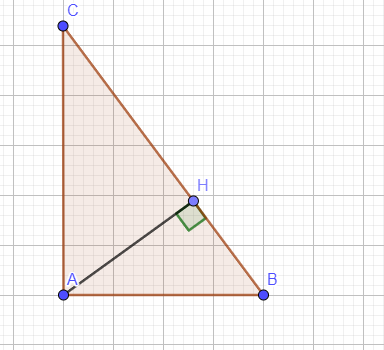
Áp dụng định lý pytago ta có :
`AC^2+AB^2=BC^2`
hay `16^2+12^2=BC^2`
`=>BC^2=400`
`=>BC=20(cm)`

Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC

a) Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow\)\(BC^2=9^2+12^2=225\)
\(\Leftrightarrow\)\(BC=\sqrt{225}=15\)cm
Diện tích tam giác ABC là:
\(S_{ABC}=\frac{AB.AC}{2}=\frac{9.12}{2}=54\)cm2
b) Xét \(\Delta ABC\)và \(\Delta HBA\) có:
\(\widehat{BAC}=\widehat{BHA}=90^0\)
\(\widehat{ABC}\) chung
suy ra: \(\Delta ABC~\Delta HBA\)
\(\Rightarrow\)\(\frac{AB}{HB}=\frac{BC}{AB}\)
\(\Rightarrow\)\(AB.AB=BH.BC\)

Bài 2
gọi E là trung điểm của KB
Vì tam giác CKB có BM=MC ; BE=EK
=>EM//KC
Vì tam giác ENM có AN=AM ; KA//EM
=>EK=KN
Vì KN=KE=EB=>NK=1/2KB

a: ΔAHB vuông tại H
=>AH<AB
ΔAHC vuông tại H
=>AH<AC
=>AH+AH<AB+AC
=>2AH<AB+AC
=>\(AH< \dfrac{1}{2}\left(AB+AC\right)\)
b: Xét ΔABC có
BM,CN là trung tuyến
BM cắt CN tại G
=>G là trọng tâm
=>BG=2GM và CG=2GN
=>BG=GE và CG=GF
=>G là trung điểm của BE và G là trung điểm của CF
Xét tứ giác BFEC có
G là trung điểm chung của BE và CF
=>BFEC là hình bình hành
=>EF=BC
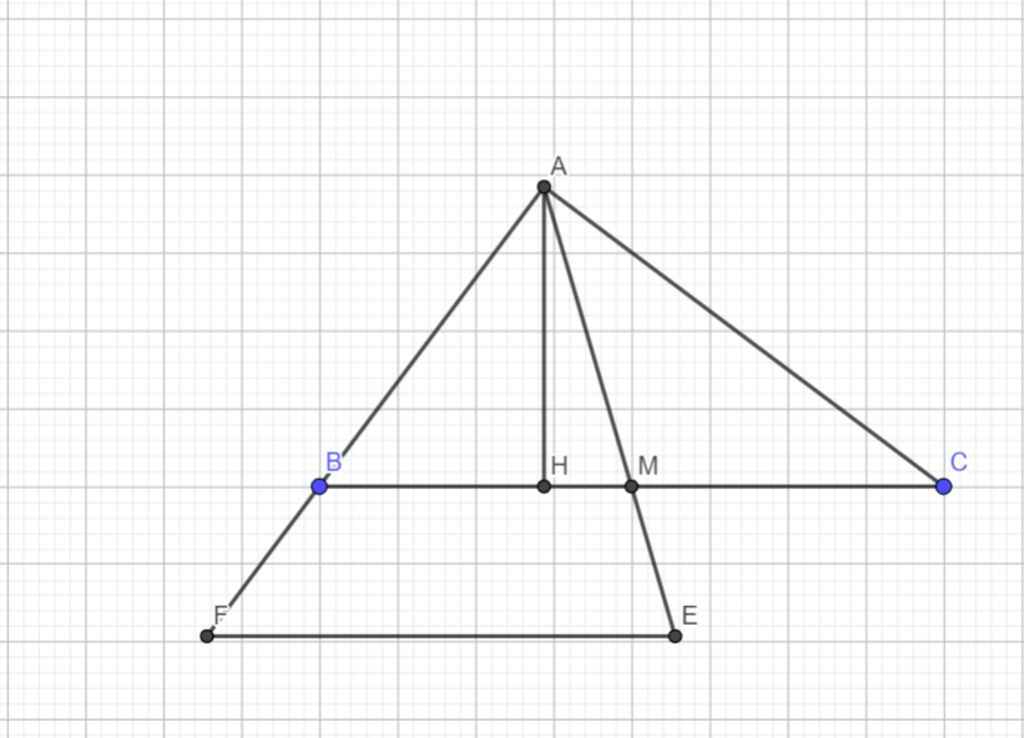
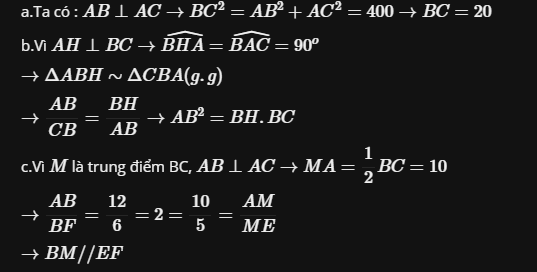
d) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=12^2+16^2=400\)
hay BC=20(cm)
Ta có: ΔABC vuông tại A(gt)
mà AM là đường trung tuyến ứng với cạnh huyền BC(gt)
nên \(AM=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
hay \(AM=\dfrac{20}{2}=10\left(cm\right)\)
Xét ΔAEF có
M\(\in\)AE(gt)
B\(\in\)AF(gt)
\(\dfrac{AM}{ME}=\dfrac{AB}{BF}\left(\dfrac{10}{5}=\dfrac{12}{6}=2\right)\)
Do đó: MB//EF(Định lí Ta lét đảo)
hay BC//EF(Đpcm)
a) Cm \(AD\cdot BC=AB\cdot DC\)
Xét ΔABC có BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AD}{DC}=\dfrac{AB}{BC}\)(Tính chất tia phân giác của tam giác)
hay \(AD\cdot BC=AB\cdot DC\)(đpcm)