Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(x;y;z\right)=\left(\dfrac{1}{a};\dfrac{1}{b};\dfrac{1}{c}\right)\Rightarrow ab+bc+ca=2020\)
BĐT trở thành:
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}+a+b+c+\sqrt{2020+a^2}+\sqrt{2020+b^2}+\sqrt{2020+c^2}\le\dfrac{2020.2021}{abc}\)
\(\Leftrightarrow\dfrac{ab+bc+ca}{abc}+a+b+c+\sqrt{2020+a^2}+\sqrt{2020+b^2}+\sqrt{2020+c^2}\le\dfrac{2020.2021}{abc}\)
\(\Leftrightarrow a+b+c+\sqrt{2020+a^2}+\sqrt{2020+b^2}+\sqrt{2020+c^2}\le\dfrac{2020^2}{abc}\)
Ta có: \(\sqrt{2020+a^2}=\sqrt{ab+bc+ca+a^2}=\sqrt{\left(a+b\right)\left(a+c\right)}\le\dfrac{1}{2}\left(2a+b+c\right)\)
Tương tự:...
\(\Rightarrow\sqrt{2020+a^2}+\sqrt{2020+b^2}+\sqrt{2020+c^2}\le2\left(a+b+c\right)\)
\(\Rightarrow a+b+c+\sqrt{2020+a^2}+\sqrt{2020+b^2}+\sqrt{2020+c^2}\le3\left(a+b+c\right)\)
Nên ta chỉ cần chứng minh:
\(3\left(a+b+c\right)\le\dfrac{2020^2}{abc}=\dfrac{\left(ab+bc+ca\right)^2}{abc}\)
\(\Leftrightarrow\left(ab+bc+ca\right)^2\ge3abc\left(a+b+c\right)\) (hiển nhiên đúng)
Dấu "=" xảy ra khi \(a=b=c\) hay \(x=y=z\)

Ta xét từng câu:
(I) Hải Phòng có phải là một thành phố trực thuộc Trung ương không?
Đây là câu hỏi, không phải mệnh đề.
(II) Hai vectơ có độ dài bằng nhau thì bằng nhau.
Đây có là mệnh đề.Mệnh đề này sai.
Hai vecto được gọi là bằng nhau nếu chúng có cùng hướng và độ dài bằng nhau.
(III) Một tháng có tối đa 5 ngày chủ nhật.
Đây có là mệnh đề và là 1 mệnh đề đúng.
(IV) 2019 là một số nguyên tố.
Đây có là mệnh đề.
Ta có : 2019= 3. 673 nên 2019 là hợp số. Mệnh đề này sai.
(V) Đồ thị của hàm số y = a x 2 ( a ≠ 0 ) là một đường parabol.
Đây là mệnh đề đúng.
(VI) Phương trình bậc hai a x 2 + b x + c = 0 ( a ≠ 0 ) có nhiều nhất là 2 nghiệm.
Đây là mệnh đề đúng.
Như vậy có tất cả 5 mệnh đề và 3 mệnh đề đúng.
Đáp án B

\(P=\dfrac{x}{\sqrt{y}}+\dfrac{y}{\sqrt{x}}\Rightarrow P^2=\dfrac{x^2}{y}+\dfrac{y^2}{x}+2\sqrt{xy}\)
\(P^2=\left(\dfrac{x^2}{y}+\sqrt{xy}+\sqrt{xy}\right)+\left(\dfrac{y^2}{x}+\sqrt{xy}+\sqrt{xy}\right)-2\sqrt{xy}\)
\(P^2\ge3x+3y-2\sqrt{xy}\ge3\left(x+y\right)-\left(x+y\right)=2\left(x+y\right)=4038\)
\(\Rightarrow P\ge\sqrt{4038}\)
Dấu "=" xảy ra khi \(x=y=\dfrac{2019}{2}\)
Ta có:
\(P=\dfrac{x}{\sqrt{2019-x}}+\dfrac{y}{\sqrt{y-2019}}=\dfrac{x}{\sqrt{y}}+\dfrac{y}{\sqrt{x}}\ge\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2}{\sqrt{x}+\sqrt{y}}=\sqrt{x}+\sqrt{y}\)
Lại có:
\(P=\dfrac{x}{\sqrt{2019-x}}+\dfrac{y}{\sqrt{2019-y}}=\dfrac{2019-y}{\sqrt{y}}+\dfrac{2019-x}{\sqrt{x}}\\ =\dfrac{2019}{\sqrt{x}}+\dfrac{2019}{\sqrt{y}}-\sqrt{x}-\sqrt{y}\)
\(\Rightarrow2P=\dfrac{2019}{\sqrt{x}}+\dfrac{2019}{\sqrt{y}}=2019\left(\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{y}}\right)\ge2019\cdot\dfrac{2}{\sqrt[4]{xy}}\\ \ge2019\dfrac{2}{\sqrt[2]{\dfrac{x+y}{2}}}=2019\cdot\dfrac{2}{\sqrt{\dfrac{2019}{2}}}=2\sqrt{2}\sqrt{2019}\)
\(\Rightarrow P\ge\sqrt{2}\sqrt{2019}\)
Dấu = khi \(x=y=\dfrac{2019}{2}\)

\(y=x^4-2018x^2-2019\) sẽ có TXĐ: D=R vì với mọi x thực thì y luôn xác định

Đáp án: A
b, c, e là mệnh đề, mệnh đề b, e là mệnh đề đúng.
Mệnh đề c sai vì π là số nhỏ hơn 4.
a, d là câu hỏi chưa biết tính đúng sai nên không là mệnh đề.


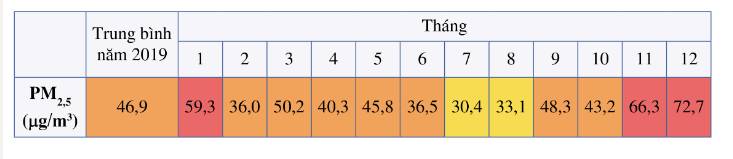
a) Từ bảng ta thấy:
Tháng 2: chỉ số \(P{M_{2,5}}\) là 36,0\(\left( {\mu g/{m^3}} \right)\)
Tháng 5: chỉ số \(P{M_{2,5}}\) là 45,8\(\left( {\mu g/{m^3}} \right)\)
Tháng 10: chỉ số \(P{M_{2,5}}\) là 43,2\(\left( {\mu g/{m^3}} \right)\)
b) Chỉ số \(P{M_{2,5}}\) là hàm số của tháng vì với mỗi tháng có đúng một chỉ số \(P{M_{2,5}}\) tương ứng.