Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
Đặt đồng vị thứ hai là: \(^a_{51}Sb\)
\(\Rightarrow\%_{^aSb}=100\%-62\%=38\%\)
Mà \(\overline{A}=121,76\)
\(\Leftrightarrow\dfrac{121.62+a.38}{100}=121,76\)
\(\Rightarrow a=123\)
Vậy nguyên tử khối của đồng vị thứ hai mà 123
Kí hiệu: \(^{123}_{51}Sb\)

1) có 18 công thức phân tử nước
2) 63Cu16O , 63Cu17O ,63Cu18O
65Cu16O ,65Cu17O .65Cu18O

1) Có 18 công thức phân tử nước
2) Có 6 công thức: 63Cu16O ; 63Cu17O ;63Cu18O
65Cu16O ; 65Cu17O ; 65Cu18O

cho anh xin lỗi nhé
a),b) có 3 loại phân tử hiđro: HH; HD ; DD
2 3 4
c)nH2=1/22.4=>MH2=0.10/(1/22.4)=2.24
=>AH=2.24/2=1.12
gọi x là % số nguyên tử 1H(100 – x) là phần trăm số nguyên tử 2H
ta có :\(\frac{x\cdot1+\left(100-x\right)\cdot2}{100}\) =1.12=>x=88%
Vậy 1H chiếm 88% số nguyên tử
2H chiếm 12% số nguyên tử
Đây là bài làm hoàn chỉnh!!
Chúc em học tốt!!
cho anh xin lỗi nhé
a),b) có 3 loại phân tử hiđro: HH; HD ; DD
2 3 4
c)nH2=1/22.4=>MH2=0.10/(1/22.4)=2.24
=>AH=2.24/2=1.12
gọi x là % số nguyên tử 1H(100 – x) là phần trăm số nguyên tử 2H
ta có :\(\frac{x\cdot1+\left(100-x\right)\cdot2}{100}\) =1.12=>x=88%
Vậy 1H chiếm 88% số nguyên tử
2H chiếm 12% số nguyên tử
Đây là bài làm hoàn chỉnh!!
Chúc em học tốt!!

a) Mg+2HCl=MgCl2+H2 (1)
theo(1) nMg=nH2=0.4/2=0.2mol
suy ra MMg=4.84/0.2=24.2g/mol
b) gọi đồng vị còn lại có số khối là Mgx12
vì tỉ số 2 đồng vị là 4:1 nên có 1 đồng vị chiếm 80%, 1 đồng vị chiếm 20%
TH1: Mg2412 chiếm 20% suy ra đồng vị còn lại chiếm 80%
Mtrung bình =24*20%+x*80%=24.2 suy ra x=24.25 (loại)
TH2:Mg2412 chiếm 80% suy ra đồng vị còn lại chiếm 20%
Mtrung bình=24*80%+x*20%=24.2 suy ra x=25
Vậy số khối của đồng vị còn lại là 25

Khối lượng nguyên tử của Cu :
\(\frac{\left(105.63+245.65\right)}{105+245}=64,4\left(g\right)\)
Vậy khối lượng của Cu là 64,4(g)

Gọi % đồng vị 21H là a: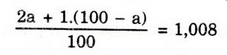
⇒ a = 0,8;
Khối lượng riêng của nước 1 g/ml, vậy 1ml nước có khối lượng 1g. Khối lượng mol phân tử của nước là 18g.


Bài 3:
- Gọi phần trăm của đồng vị \(^6Li\) là x (%)
=> \(\%^7Li=100-x\left(\%\right)\)
=> \(A_{Li}=\dfrac{6x+7.\left(100-x\right)}{100}\\ \Leftrightarrow6,94=\dfrac{6x+700-7x}{100}\\ \Leftrightarrow6,94.100=6x+700-7x\\ \Leftrightarrow7x-6x=700-694\\ \Leftrightarrow x=6\)
=> \(\left\{{}\begin{matrix}\%^6Li=6\%\\\%^7Li=100\%-6\%=94\%\end{matrix}\right.\)