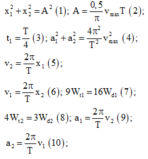Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
+ Ta để ý rằng, trong dao động điều hòa thì li độ và vận tốc luôn vuông pha nhau
+ Hai thời điểm t 1 và t 2 vuông pha nhau do vậy v 2 sẽ ngược pha với x 1 , ta có v 2 x 1 = b x 1 = ω = π rad.
Tương tự, thời điểm t 3 ngược pha với t 2 nên ta có
v 3 v 2 = 1 ⇔ b + 8 π b = 1 ⇒ b + 8 π b = − 1 ⇒ b = − 4 π
Thay vào biểu thức trên ta tìm được x 1 = 4 cm

Đáp án D
Áp dụng công thức: 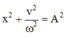 .
.
Khi tốc độ của chất điểm là 10 π 2 cm/s thì x = 10 2 cm
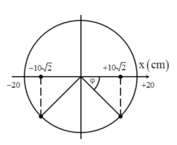
+ Tại thời điểm t1 vật ở vị trí cân bằng với x = 0
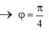
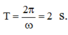
Thời gian lớn nhất để vật lại đạt được vị trí có x = 10 2 cm với
Dt < 2015T tương ứng với vị trí của điểm A nên:
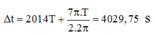

Đáp án B
+ Áp dụng hệ thức độc lập thời gian giữa vận tốc và gia tốc, ta có:
v 1 ωA 2 + a 1 ω 2 A = 1 v 2 ωA 2 + a 2 ω 2 A = 1 → 10 3 ωA 2 + − 100 ω 2 A 2 = 1 − 10 ωA 2 + − 3 . 100 ω 2 A 2 = 1
→ ω = 10 A = 2
+ Li độ x 2 của vật tại thời điểm t 2 :
x 2 = A 2 − v 2 ω 2 = 2 2 − − 10 10 2 = 3

Chọn A
Thay cặp (x1, v1) và (x2, v2) vào hệ thức liên hệ giữa v và x:
A
2
-
v
2
w
2
=
x
2
ta được hệ phương trình hai ẩn
A
2
và
1
w
2
. Giải hệ phương trình ta được:
+ A 2 = 36 ⇒ A = 6 c m .
+ 1 w 2 = 1 400 ⇒ w = 20 r a d / s .