Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1 là vuông góc với AB chứ không phải vuông góc với A nha. Mình đánh nhanh nên nhầm

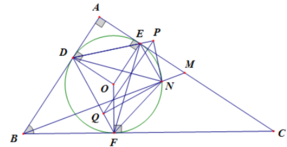
Vì DPN+DQN=90o+90o=180o nên DPNQ là tứ giác nội tiếp
=>QPN=QDN (hai góc nội tiếp cùng chắn cung QN) (5)
Mặt khác DENF là tứ giác nội tiếp nên QDN=FEN (6)
Từ (5) và (6) ta có FEN=QPN (7)
Tương tự ta có: EFN=PQN (8)
Từ (7) và (8) suy ra Δ N P Q ~ Δ N E F ( g . g ) = > P Q E F = N Q N F
Theo quan hệ đường vuông góc – đường xiên, ta có
N Q ≤ N F = > P Q E F = N Q N F ≤ 1 = > P Q ≤ E F
Dấu bằng xảy ra khi Q ≡ F ⇔ NF ⊥ DF ⇔ D, O, N thẳng hàng.
Do đó PQ max khi M là giao điểm của AC và BN, với N là điểm đối xứng với D qua O.

Cậu ơi cho t hỏi tí: câu (a) ấy cái chỗ c/m AD vuông góc vs BC trình bày kiểu gì cho nó logic được ???
Xét tứ giác AEDF có
AE//DF
DE//AF
Do đó: AEDF là hình bình hành
Suy ra: Hai đường chéo AD và EF cắt nhau tại trung điểm của mỗi đường
mà O là trung điểm của FE
nên O là trung điểm của AD
=>Khi D di chuyển trên BC thì O là trung điểm của AD