Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

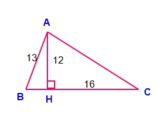
A C B H
Áp dụng định lý Pytago ta có:
\(AC^2=AH^2+HC^2=12^2+16^2=400\)
\(\Rightarrow AC=20\left(cm\right)\)
Và \(BH^2=AB^2-AH^2=13^2-12^2=25\)
\(\Rightarrow BH=5\left(cm\right)\Rightarrow BC=BH+HC=5+16=21\left(cm\right)\)
Vậy \(\hept{\begin{cases}AC=20\left(cm\right)\\BC=21\left(cm\right)\end{cases}}\)

Câu 1:
Xét tam giác ABH vuông tại H, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
202 = AH2 + 162
400 = AH2 + 256
AH2 = 400 - 256
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
AC2 = 122 + 52
AC2 = 144 + 25
AC2 = 169
AC = \(\sqrt{169}\)= 13 (cm)
Vậy AH = 12 cm
AC = 13 cm
Bài 2:
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
152 = AH2 + 92
225 = AH2 + 81
AH2 = 225 - 81
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHB vuông tại, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
AB2 = 122 + 52
AB2 = 144 + 25
AB2 = 169
AB = \(\sqrt{169}\)= 13 (cm)
Vậy AB = 13 cm

Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow AC^2=12^2+16^2=400\)
hay AC=20(cm)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow HB^2=AB^2-AH^2=13^2-12^2=25\)
hay HB=5(cm)
Ta có: HB+HC=BC(H nằm giữa B và C)
nên BC=5+16=21(cm)
Vậy: AC=20cm; BC=21cm

AH \(\perp\) BC ( gt )
\(\Rightarrow\) Tam giác HAC vuông tại H
\(\Rightarrow\) \(^{AC^2}\) = \(^{AH^2}\) + \(^{HC^2}\)
\(\Rightarrow\) \(^{AC^2}\)= \(^{12^2}\) + \(^{16^2}\)
\(\Rightarrow\) \(^{AC^2}\)= 144 + 256
\(\Rightarrow\) \(^{AC^2}\)= 400
\(\Rightarrow\) AC = 20 ( cm )
AH \(\perp\) BC ( gt )
\(\Rightarrow\) Tam giác HAB vuông tại H
\(\Rightarrow\) \(AB^2\) = \(AH^2\) + \(BH^2\)
\(\Rightarrow\) \(BH^2\) = \(AB^2\) - \(AH^2\)
\(\Rightarrow\) \(BH^2\) = \(13^2\) - \(12^2\)
\(\Rightarrow\) \(BH^2\) = 169 - 144
\(\Rightarrow\) \(BH^2\) = 25
\(\Rightarrow\) BH = 5 ( cm )
Có: BH + HC = BC ( Vì H nằm giữa B và C )
\(\Rightarrow\) 5 + 16 = 21 ( cm )
Vậy AC = 20 cm
BC = 21 cm
Học tốt

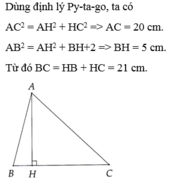
Áp dụng định lí Pi-ta-go trong ΔAHC vuông tại H ta có:
AC2 = AH2 + HC2 = 122 + 162 = 144 + 256 = 400
⇒ AC = 20 (cm)
Áp dụng định lí Pi-ta-go trong ΔAHB vuông tại H ta có:
BH2 + AH2 = AB2 ⇒ BH2 = AB2 - AH2 = 132 - 122 = 169 -144 = 25
⇒ BH = 5cm
Do đó BC = BH + HC = 5 + 16 = 21 (cm)

CÂU 2
A B C E F K 1 1 2 2
a) Xét tam giác BEC và tam giác CFB có:
BC chung
E1=F1=90 độ(Vì BE vg góc vs AC:CF vg góc vs AB)
Góc B= góc C(Vì tam giác ABC cân tại A)
=>Xét tam giác BEC = tam giác CFB(CH-GN)
b) Vì tam giác BEC = tam giác CFB(cm a)
=>\(\widehat{KCB}=\widehat{KBC}\)( Hai góc tứ)
=> Tam giác KBC cân tại K
bn ơi ! đề kiểu j vậy :v ko hiểu
bạn ơi mik gửi đề mới lên rồi nhé