Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
Cắt khối đa diện đã cho làm hai khối: khối lăng trụ và khối tứ diện.
Cách giải:
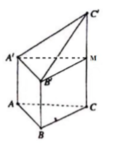
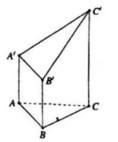
Gọi M là trung điểm của CC’.
Khi đó: khối đa diện đã cho được chia làm 2 phần: Khối lăng trụ tam giác đều A’B’M.ABC và khối tứ diện A’B’C’M.
Thể tích khối lăng trụ tam giác đều A’B’M.ABC là:
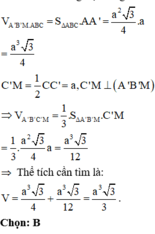

Đáp án A.
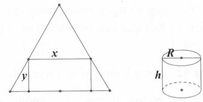
Gọi cạnh đáy của khối chóp là x với
0 < x < 5 2 2 .
Chiều cao của khối chóp là
h = 5 2 2 − x 2 2 − x 2 2 = 25 − 5 x 2 2 .
Vậy thể tích của khối chóp là
V = 1 3 . h . S = 1 3 . x 2 . 25 − 5 x 2 2 = 1 3 25 x 4 − 5 x 5 2 2 .
Xét hàm số f x = 25 x 4 − 5 x 5 2 trên 0 ; 5 2 2 ,
ta có f ' x = 100 x 3 − 25 x 4 2 = 0 ⇔ x = 2 2 .
Suy ra giá trị lớn nhất của thể tích là V = 1 3 . f 2 2 2 = 4 10 3 .

Đáp án là D.
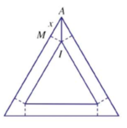
M I = x 3 3 ; S t g = a − 2 x 2 3 4 .
V l t = M I . S t g = a 2 x − 4 a x 2 + 4 x 3 4 ; 0 < x < a 2 .
xét hàm số
f x = 4 x 3 − 4 a x 2 + a 2 x ⇒ f ' x = 12 x 2 − 8 a x + a 2 , cho f ' x = 0 ⇔ x = a 6 x = a 2 l o a i
Thể tích đạt GTLN khi x = a 6 .

Đáp án B

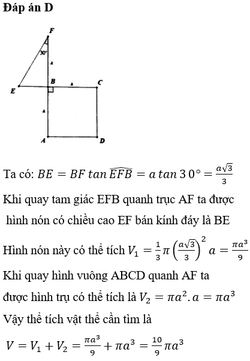
Bán kính đáy của nón bằng bán kính đường tròn nội tiếp hình vuông ABCD suy ra r = A D 2 = a ; H A = A C 2 = a 2
Chiều cao nón:
h = S A 2 − H A 2 = 4 a 2 − a 2 2 = a 2
Do đó V = π r 2 h 3 = π 2 a 3 3

Chọn B.
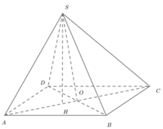
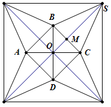
Phương pháp: Mấu chốt bài toán là chỉ ra được tam giác SAC vuông tại S.
Cách giải: Gọi O là giao điểm của AC và BD, H là hình chiếu của S lên mặt đáy.




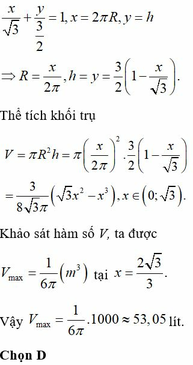
Chọn A