Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Chọn toa có 3 người có 3 (toa)
Chọn 3 hành khách xếp vào toa đó có ![]() (cách)
(cách)
Hành khách còn lại có 2 cách chọn toa
Số cách chọn là: 3. ![]() .2 = 24 (C).
.2 = 24 (C).

Không gian mẫu: mỗi khách có 12 cách chọn toa nên 7 khách có \(12^7\) cách lên tàu
Chọn 3 tỏa từ 12 toa: có \(C_{12}^3\) cách
- Xếp 7 khách vào 3 toa theo cách bất kì: mỗi khách có 3 cách chọn toa nên có \(3^7\) cách
- Chọn 2 toa từ 3 toa có \(C_3^2\) cách, xếp 7 khách vào 2 toa này có \(2^7\) cách \(\Rightarrow C_3^2.2^7\) cách xếp 7 khách vào không nhiều hơn 2 toa
- Chọn 1 toa có 3 cách, xếp 7 khách vào toa này có \(1^7=1\) cách \(\Rightarrow3\) cách xếp 7 khách vào 1 toa
\(\Rightarrow C_{12}^3\left(3^7-C_3^2.2^7+3\right)\) cách xếp 3 toa đều có khách
Xác suất: \(P=\dfrac{C_{12}^3\left(3^7-C_3^2.2^7+3\right)}{12^7}=0,011\)

a. Có 5 cách chọn 1 toa cho 6 người
b. Mỗi người có 5 cách chọn toa, do đó 6 người có \(5^6\) cách chọn

Số cách lên toa của 7 người là: 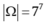
Ta tìm số khả năng thuận lợi của A như sau
Chọn 3 toa có người lên: ![]()
Với toa có 4 người lên ta có: ![]() cách chọn
cách chọn
Với toa có 2 người lên ta có: ![]() cách chọn
cách chọn
Người cuối cùng cho vào toa còn lại nên có 1 cách
Theo quy tắc nhân ta có: ![]()
Do đó: 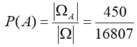 .
.
Chọn A.

Chọn 3 hành khách từ 4 hành khách: có \(C_4^3=4\) cách
Xếp nhóm 3 hành khách này vào 1 toa trong 3 toa: có 3 cách
Xếp hành khách còn lại vào 2 toa còn lại: có 2 cách
Vậy tổng cộng có \(4.3.2=24\) cách

Mỗi hành khách có 8 cách chọn toa tàu để lên, do đó không gian mẫu là: \(8^3\)
Chọn 3 toa trong 8 toa và xếp 3 hành khách vào 3 toa đó (mỗi hành khách 1 toa): \(A_8^3\) cách
Xác suất: \(\dfrac{A_8^3}{8^3}=\dfrac{21}{32}\)

Không gian mẫu: \(n_{\Omega}=3^5\)
Gọi biến cố A: Toa nào cũng có người lên
TH1: 1 toa có 3 khách, 2 toa còn lại 1 khách
Có: \(C^1_3\cdot C^3_5\cdot2=60\) cách
TH2: Một toa có 1 khách 2 toa còn lại mỗi toa có 2 khách.
Có: \(C^1_3.C^1_5.C^4_2=90\)cách
\(\Rightarrow n\left(A\right)=150cách\)
\(\Rightarrow P\left(A\right)=\dfrac{150}{3^5}=\dfrac{50}{81}\)
người A có 2 cách chọn
với mỗi cách chọn người A thì người B có 2 cách chọn
với mỗi cách chọn người A,B thì người C có 2 cách
theo quy tắc nhân có 8 cách
(nếu sai bạn thông cảm nhé)