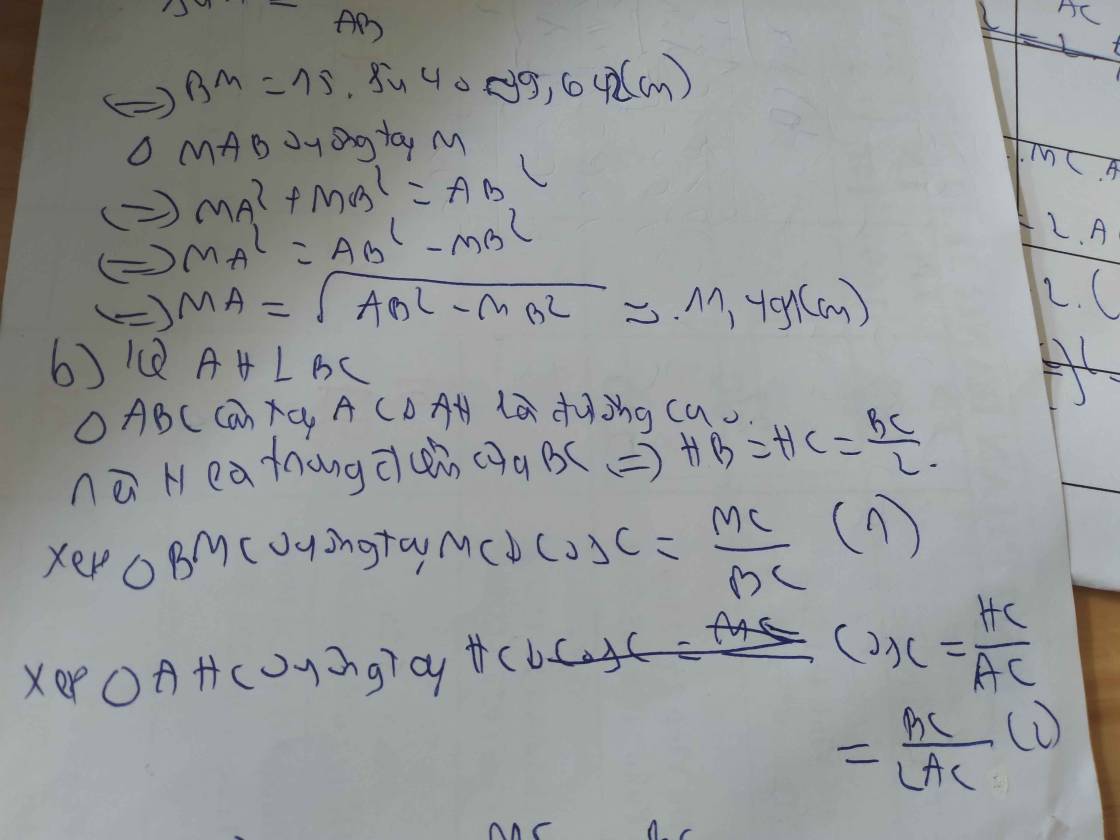Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 9:
a) Ta có: \(9x^2-16=0\)
\(\Leftrightarrow\left(3x-4\right)\left(3x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{4}{3}\\x=-\dfrac{4}{3}\end{matrix}\right.\)
b) Ta có: \(4x^2=13\)
\(\Leftrightarrow x^2=\dfrac{13}{4}\)
\(\Leftrightarrow x\in\left\{\dfrac{\sqrt{13}}{2};-\dfrac{\sqrt{13}}{2}\right\}\)
c) Ta có: \(2x^2+9=0\)
\(\Leftrightarrow2x^2=-9\)(Vô lý)
d) Ta có: \(-x^2+324=0\)
\(\Leftrightarrow x^2=324\)
\(\Leftrightarrow\left[{}\begin{matrix}x=18\\x=-18\end{matrix}\right.\)


b)\(\Delta DBC\) vuông tại B có đường cAO BA nên
\(\dfrac{1}{AB^2}=\dfrac{1}{BD^2}+\dfrac{1}{BC^2}\)
\(\Leftrightarrow\dfrac{1}{BD^2}=\dfrac{1}{3^2}-\dfrac{1}{5^2}=\dfrac{16}{225}\)
\(\Leftrightarrow BD=\dfrac{15}{4}\left(cm\right)\)
\(AD=\sqrt{BD^2-AB^2}=\dfrac{9}{4}\left(cm\right)\)
c)\(\Delta ABD\) vuông tại A có đường cao AF nên
\(BF.BD=AB^2\left(1\right)\)
\(\Delta BAC\) vuông tại có đường cao AE nên
\(BE.BC=AB^2\left(2\right)\)
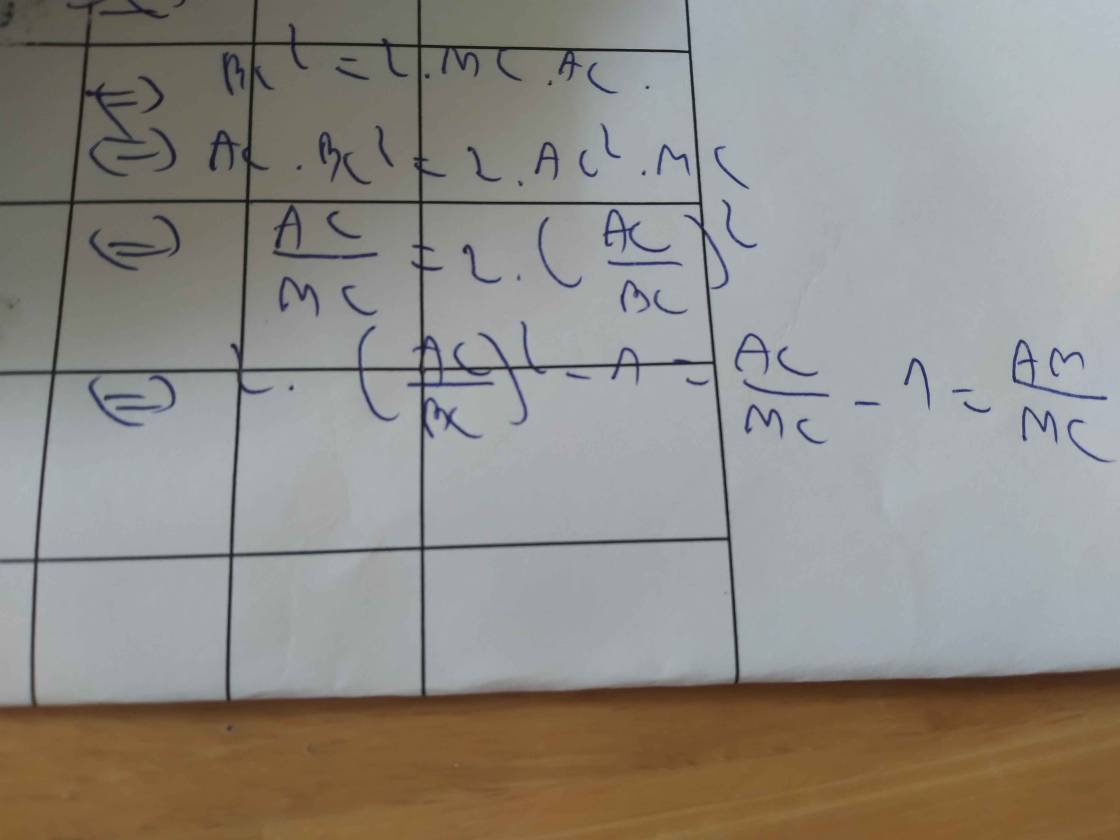
từ \(\left(1\right)và\left(2\right)\Rightarrow BF.BD=BE.BC\)

để em viết ra vậy ạ
cho tam giac mnp vuông tại m (mn>mp) có đường cao mk
a) biết mn=20cm, mp=15cm, tính mk và góc mnp (góc làm tròn đến đơn vị phút).
b) vẽ trung tuyến me của tam giác mnp. từ p vẽ đường thẳng vuông góc với me cắt mn tại d. cm tam giác mnp đồng dạng với tam giác mpd, từ đó suy ra mn.md=np.pk

Bài 5:
a: Ta có: \(m^2+1>0\forall m\)
nên hàm số \(y=2\left(m^2+1\right)x+1\) luôn là hàm số bậc nhất
b: Ta có: \(m^2+1>0\forall m\)
nên ham số \(y=\sqrt{m^2+1}x-\sqrt{m^2+1}\) luôn là hàm số bậc nhất

a.
d đi qua A nên:
\(1\left(m+1\right)-2m+3=2\)
\(\Rightarrow m=2\)
b.
Em tự vẽ
c.
Giả sử điểm cố định mà d luôn đi qua là \(M\left(x_0;y_0\right)\), khi đó với mọi m ta luôn có:
\(y_0=\left(m+1\right)x_0-2m+3\)
\(\Leftrightarrow m\left(x_0-2\right)+x_0-y_0+3=0\)
\(\Rightarrow\left\{{}\begin{matrix}x_0-2=0\\x_0-y_0+3=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_0=2\\y_0=5\end{matrix}\right.\) \(\Rightarrow M\left(2;5\right)\)
d.
- Với \(m=-1\Rightarrow\) d không cắt y=2
- Với \(m\ne-1\)
\(\Rightarrow\left(m+1\right)x-2m+3=2\)
\(\Rightarrow\left(m+1\right)x=2m-1\)
\(\Rightarrow x=\dfrac{2m-1}{m+1}\)
Tọa độ giao điểm của d và y=2 là: \(\left(\dfrac{2m-1}{m+1};2\right)\)

Bài 1:
\(a,\Leftrightarrow m-1\ne0\Leftrightarrow m\ne1\\ b,\Leftrightarrow m-1>0\Leftrightarrow m>1\\ c,\Leftrightarrow m-1< 0\Leftrightarrow m< 1\)
Bài 2:
\(a,\text{Đồng biến}\Leftrightarrow2m>0\Leftrightarrow m>0\\ \text{Nghịch biến}\Leftrightarrow m-1< 0\Leftrightarrow m< 1\\ b,\Leftrightarrow\left\{{}\begin{matrix}2m=m-1\\m+1\ne3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-1\\m\ne2\end{matrix}\right.\Leftrightarrow m=-1\)


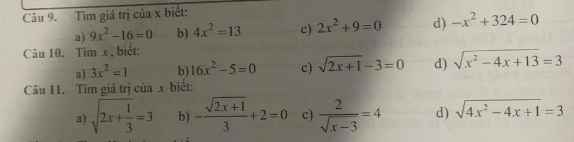





 em cần giải gấp câu b,c theo hệ thức lượng cần gấp ạ
em cần giải gấp câu b,c theo hệ thức lượng cần gấp ạ
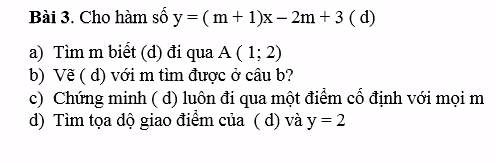


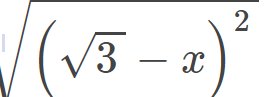
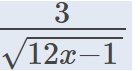 GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ
GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ giúp em với ạ, cần gấp ạ TvT
giúp em với ạ, cần gấp ạ TvT