
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Gọi \(A=1-x^2\)
Ta có: \(x^2\ge0\Rightarrow-x^2\le0\Rightarrow A=1-x^2\le1\)
Dấu " = " khi \(x^2=0\Rightarrow x=0\)
Vậy \(MAX_A=1\) khi x = 0
b) Đặt \(B=-3y^2\)
Ta có: \(3y^2\ge0\Rightarrow-3y^2\le0\)
Dấu " = " khi \(-3y^2=0\Rightarrow y=0\)
Vậy \(MAX_B=0\) khi y = 0
c) Đặt \(C=10-\left(2x-1\right)^2\)
Ta có: \(\left(2x-1\right)^2\ge0\)
\(\Rightarrow-\left(2x-1\right)^2\le0\)
\(\Rightarrow10-\left(2x-1\right)^2\le10\)
Dấu " = " khi \(\left(2x-1\right)^2=0\Rightarrow2x-1=0\Rightarrow x=\frac{1}{2}\)
Vậy \(MAX_C=10\) khi \(x=\frac{1}{2}\)

Em vào đây nhé Vẽ hình trực tuyến trên hoc24 | Hướng dẫn tạo khóa học trên hoc24 | Học trực tuyến
Vẽ hình trực tuyến trên hoc24 | Hướng dẫn tạo khóa học trên hoc24 | Học trực tuyến
Ấn vào cái chữ màu xanh nhé!

3. Xét tam giác ADM và tam giác AEM có :
góc ADM = góc AEM = 90 độ
Góc BAM = góc CAM (gt)
AM chung
=>Tam giác ADM = tam giác AEm (c.huyền - g.nhọn)
=>MD = ME (cặp cạnh t/ứng )
AD = AE (cặp cạnh t/ứng )
Xét tam giác MDB và tam giác MEC có :
MB = MC (gt)
góc MDB = góc MEC = 90 độ
MD = ME ( câu a)
=>Tam giác MDB = Tam giác MEC (c.huyền-c.g.vuông)
Vì AD + DB = AB
AE + EC = AC
Mà AD = AE
DB = EC
=>AB = AC
Xét tam giác ABM và tam giác ACM có
AM chung
góc BAM = góc CAM (gt)
AB = AC (CMT)
=>Tam giác ABM = Tam giác ACM (c.huyền-g.nhon)
Vậy có 3 cặp tam giác bằng nhau

Câu hỏi của Nguyễn Trọng Phúc - Toán lớp 7 | Học trực tuyến

\(\left(x-3\right)^2+\left|y^2-9\right|=0\)
Vì \(\left\{{}\begin{matrix}\left(x-3\right)^2\ge0\forall x\\\left|y^2-9\right|\ge0\forall y\end{matrix}\right.\)
để bt = 0 \(\Leftrightarrow\left\{{}\begin{matrix}\left(x-3\right)^2=0\\\left|y^2-9\right|=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\y^2-9=0\Rightarrow y^2=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\\left[{}\begin{matrix}y=3\\y=-3\end{matrix}\right.\end{matrix}\right.\)
Vậy.....
\(\left(x-3\right)^2+\left|y^2-9\right|=0\)
\(\Rightarrow\left[{}\begin{matrix}\left(x-3\right)^2=0\\\left|y^2-9\right|=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x-3=0\\y^2-9=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\y^2=9\left[{}\begin{matrix}y=3\\y=-3\end{matrix}\right.\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=3\\y=3hoặcy=-3\end{matrix}\right.\)

Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó

\(x-y=9\Rightarrow x=9+y\Rightarrow y=x-9\)
Ta có:
\(\dfrac{4x-9}{3x+y}-\dfrac{4y+9}{3y+x}\)
\(=\dfrac{3x+x-9}{3x+y}-\dfrac{3y+y+9}{3y+x}\)
\(=\dfrac{3x+\left(x-9\right)}{3x+y}-\dfrac{3y+\left(y+9\right)}{3y+x}\)
\(=\dfrac{3x+y}{3x+y}-\dfrac{3y+x}{3y+x}\)
\(=1-1\)
\(=0\)
Vậy biểu thức \(\dfrac{4x-9}{3x+y}-\dfrac{4y+9}{3y+x}\)khi \(x-y=9\) là 0
\(x-y=9\Rightarrow y=x-9\) thay vào biểu thức B ta được :
\(B=\dfrac{4x-9}{3x+\left(x-9\right)}-\dfrac{4\left(x-9\right)+9}{3\left(x-9\right)+x}=\dfrac{4x-9}{4x-9}-\dfrac{4x-27}{4x-27}=1-1=0\)
Vậy giá trị của B là 0 tại \(x-y=9\)
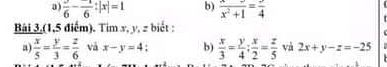

 M.n giải hộ em vs đg cần gấp ạ
M.n giải hộ em vs đg cần gấp ạ
Bài 3:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{z}{6}=\dfrac{x-y}{5-3}=\dfrac{4}{2}=2\)
Do đó: x=10; y=6; z=12
a) Áp dụng t/c dtsbn:
\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{z}{6}=\dfrac{x-y}{5-3}=\dfrac{4}{2}=2\)
\(\Rightarrow\left\{{}\begin{matrix}x=2.5=10\\y=2.3=6\\z=2.6=12\end{matrix}\right.\)
b) \(\Rightarrow\dfrac{x}{6}=\dfrac{y}{8}=\dfrac{z}{15}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{6}=\dfrac{y}{8}=\dfrac{z}{15}=\dfrac{2x}{12}=\dfrac{2x+y-z}{12+8-15}=\dfrac{-25}{5}=-5\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-5\right).6=-30\\y=\left(-5\right).8=-40\\z=\left(-5\right).15=-75\end{matrix}\right.\)