Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
Công thức tính thể tích của khối trụ có bán kính đáy R và chiều cao h: V = π R 2 h
Công thức tính thể tích của khối nón có bán kính đáy R và chiều cao h: V = 1 3 π R 2 h
Cách giải:
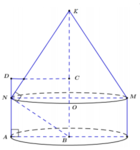
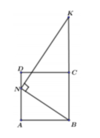
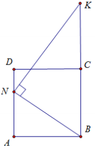
Khi quay tứ giác ANKB quanh trục BK ta được hình trụ có bán kính đáy AB, chiều cao AN và hình nón có bán kính đáy AB, chiều cao K O = B K − A N
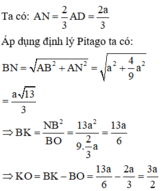
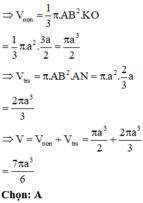

Đáp án D
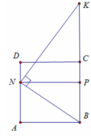
Gọi P là hình chiếu của N xuống BK
Khi quay tứ giác ANPB quanh trục BC ta được khối trụ có thể tích V 1 = πAB 2 . BP = 2 a 3 π 3
Lại có B P = 2 3 a ; N P = a suy ra P K = N P 2 B P = 3 a 2
Khi quay tam giác NKP quanh trục BC ta được khối nón có thể tích do đó V = V 1 + V 2 = 7 6 πa 3

Hình bạn tự vẽ nhé !
a) Trên cùng 1 nửa mặt phẳng bờ Ox có xOz < xOy (vì 20o < 100o) nên tia Oz nằm giữa 2 tia Ox và Oy.
b) Vì tia Oz nằm giữa 2 tia Ox và Oy nên :
xOz + zOy = xOy, thay số :
20o + zOy = 100o
zOy = 100o - 20o = 80o
Vì tia Om là tia phân giác của zOy nên :
zOm = mOy = \(\frac{zOy}{2}\) = \(\frac{80^o}{2}\) = 40o
Vì tia Oz nằm giữa 2 tia Ox và Om nên :
xOz + zOm = xOm, thay số :
20o + 40o = xOm
60o = xOm
Vậy xOm=60o.
Có gì sai thì bạn bỏ qua nhé !![]() Chúc bạn học tốt !
Chúc bạn học tốt ! ![]()

A) Ta có AB2 + AC2 = BC2 => AB2 = BC2 - AC2 = 100 - 36 => AB = 8cm
B) AM = BM (Do CM là trung tuyến của tam giác ABC)
CM = MD (Theo đề bài)
góc AMC = BMD (hai góc đối đỉnh)
=> Tam giác MAC = tam giác MBD (cgc)
=> AC = BD (Hai cạnh tương ứng của hai tam giác bằng nhau)
C) Ta có BC + BD > CD
=> BC + AC > 2 CM


mình cũng ko biết
Bạn bị trừ điểm rùi