
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: 1 - 4 x + 4 x 2 = 5 ⇔ 1 - 2 x 2 = 5
⇔ |1 - 2x| = 5 (3)
* Trường hơp 1: 1 - 2x ≥ 0 ⇔ 2x ≤ 1 ⇔ x ≤ 1/2 ⇒ |1 - 2x| = 1 - 2x
Suy ra: 1 - 2x = 5 ⇔ -2x = 5 - 1 ⇔ x = -2
Giá trị x = -2 thỏa mãn điều kiện x ≤ 1/2
Vậy x = -2 là nghiệm của phương trình (3).
* Trường hợp 2: 1 - 2x < 0 ⇔ 2x > 1 ⇔ x > 12 ⇒ |1 - 2x| = 2x - 1
Suy ra: 2x - 1 = 5 ⇔ 2x = 5 + 1 ⇔ x = 3
Giá trị x = 3 thỏa mãn điều kiện x > 1/2
Vậy x = 3 là nghiệm của phương trình (3).
Vậy x = -2 và x = 3.

4 x 2 - 4 x + 1 = 3
⇔ 2 x - 1 2 = 3 ⇔ 2 x - 1 = 3
⇔ [ 2 x - 1 = 3 2 x - 1 = - 3
Nên x = 2 hoặc x = -1
Vậy phương trình có nghiệm x = 2; x = - 1

Câu 7:
\(\sqrt{\left(2x-1\right)^2}=\left|2x-1\right|\)
\(=\left|2\cdot5-1\right|=9\)

căn
- Với x ≥ 3 thì |x - 3| = x - 3 nên ta được:
x - 3 = 9 ⇔ x = 12
- Với x < 3 thì |x - 3| = 3 - x nên ta được:
3 - x = 9 ⇔ x = -6
Vậy phương trình có hai nghiệm: x = 12; x = -6
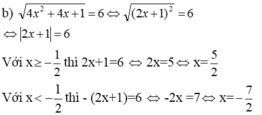

2: =>2x^2-8x+4=x^2-4x+4 và x>=2
=>x^2-4x=0 và x>=2
=>x=4
3: \(\sqrt{x^2+x-12}=8-x\)
=>x<=8 và x^2+x-12=x^2-16x+64
=>x<=8 và x-12=-16x+64
=>17x=76 và x<=8
=>x=76/17
4: \(\sqrt{x^2-3x-2}=\sqrt{x-3}\)
=>x^2-3x-2=x-3 và x>=3
=>x^2-4x+1=0 và x>=3
=>\(x=2+\sqrt{3}\)
6:
=>\(\sqrt{\left(\sqrt{x-1}+1\right)^2}-\sqrt{\left(\sqrt{x-1}-1\right)^2}=-2\)
=>\(\sqrt{x-1}+1-\left|\sqrt{x-1}-1\right|=-2\)
=>\(\left|\sqrt{x-1}-1\right|=\sqrt{x-1}+1+2=\sqrt{x-1}+3\)
=>1-căn x-1=căn x-1+3 hoặc căn x-1-1=căn x-1+3(loại)
=>-2*căn x-1=2
=>căn x-1=-1(loại)
=>PTVN
1) ĐK: \(x\ge\dfrac{5}{2}\)
pt <=> \(x-4=\sqrt{2x-5}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge4\\\left(x-4\right)^2=2x-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge4\\x^2-8x+16=2x-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge4\\x^2-10x+21=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge4\\\left(x-3\right)\left(x-7\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge4\\\left[{}\begin{matrix}x=3\left(l\right)\\x=7\left(n\right)\end{matrix}\right.\end{matrix}\right.\)
Vậy, pt có nghiệm duy nhất là x=7
2) ĐK: \(2x^2-8x+4\ge0\)
pt <=> \(\left\{{}\begin{matrix}x\ge2\\2x^2-8x+4=x^2-4x+4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge2\\x^2-4x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge2\\x\left(x-4\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge2\\\left[{}\begin{matrix}x=0\left(l\right)\\x=4\left(n\right)\end{matrix}\right.\end{matrix}\right.\)
Vậy, pt có nghiệm duy nhất là x=4
3) ĐK: \(x\ge3\)
pt <=> \(\left\{{}\begin{matrix}x\le8\\x^2+x-12=x^2-16x+64\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le8\\17x=76\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le8\\x=\dfrac{76}{17}\left(n\right)\end{matrix}\right.\)
Vậy, pt có nghiệm duy nhất là \(x=\dfrac{76}{17}\)\(\)
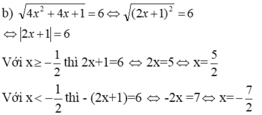
\(\sqrt{4x^2-4x+1}=x-1\)
\(\Leftrightarrow\sqrt{\left(2x-1\right)^2}=x-1\)
\(\Leftrightarrow\left|2x-1\right|=x-1\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=x-1\\2x-1=1-x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{2}{3}\end{matrix}\right.\)
\(\sqrt{4x^2-4x+1}=x-1\)
\(\left|2x-1\right|=x-1\)
TH1: \(x< \dfrac{1}{2}\) phương trình trên trở thành:
\(1-2x=x-1\Leftrightarrow x=\dfrac{2}{3}\) (không thỏa mãn \(x< \dfrac{1}{2}\))
TH2: \(x\ge\dfrac{1}{2}\) phương trình trên trở thành:
\(2x-1=x-1\Leftrightarrow x=0\) (không thỏa mãn \(x\ge\dfrac{1}{2}\))
Vậy phương trình đã cho vô nghiệm.