Question

[☠✔AFK✪Kaito Kid✔☠]

các chữ số tận cùng khi nâng lên lũy thừa

Answer 1

[cô của đơn]

1.Chữ số tận cùng của các số tự nhiên có tận cùng bằng 0;1;5;6 khi nâng lên lũy thừa: 

1. 1. • 
        Cho HS tính các lũy thừa sau ( Sử dụng máy tính) 

 Các số tự nhiên có chữ số tận cùng là 0;1;5;6 khi nâng lên lũy thừa bất kì( 0) thì giữ nguyên chữ số tận cùng của nó. 

Ví dụ: Tìm chữ số tận cùng của các lũy thừa sau:

a) 156 ⁷ ; b)1061 ⁹

c) 156 ⁷ + 1061 ⁹ d) 156 ⁷ . 1061 ⁹ 

 Giáo Viên hướng dẫn Học Sinh áp dụng tính chất trên:

a) 156 ⁷ có chữ số tận cùng là 6

b) 1061 ⁹ có chữ số tận cùng là 1

c) Theo câu a) và b)  Chữ số tận cùng của lũy thừa :156 ⁷ + 1061 ⁹ là 7

1. 
   Theo kết quả câu a) và b)  Chữ số tận cùng của lũy thừa :156 ⁷ .1061 ⁹ là 6. 

Các bài tập tương tự: 

1. 
   71³⁰ ;b) 26 ³⁵ ; c) 86 ³³ 

d) 71 ³⁰ + 26 ³⁵; ;f) 

g) 71 ³⁰ + 26 ³⁵ ; h ) 86 ³³ . 71 ³⁰ ; k) +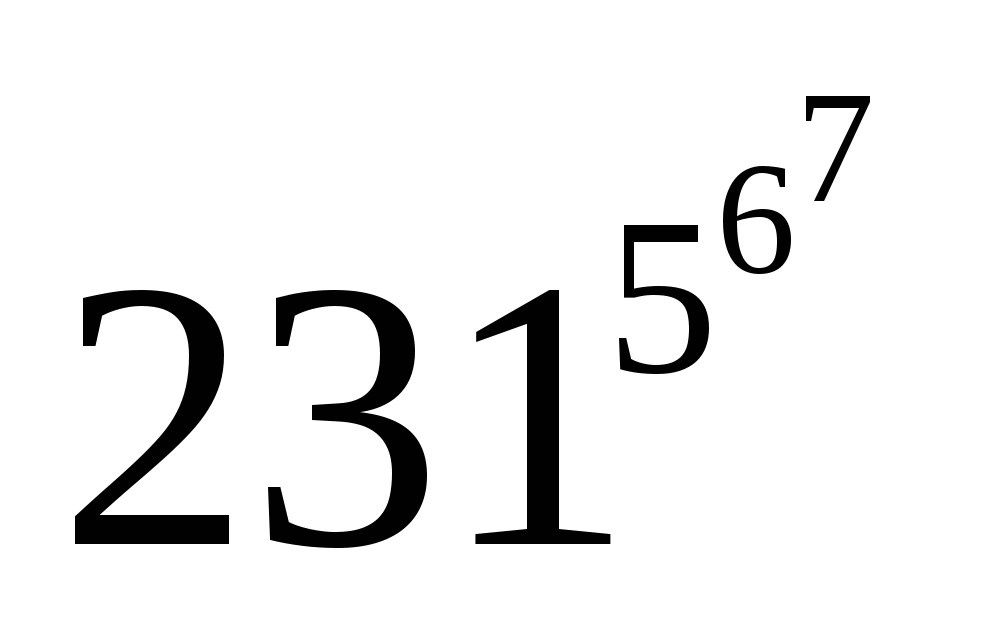 

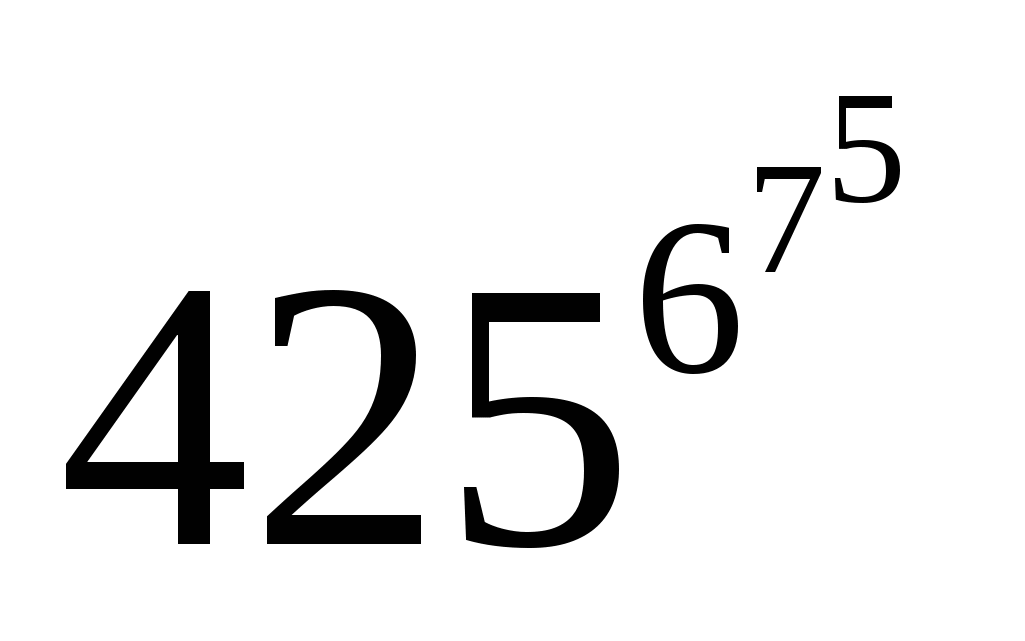
2.Chữ số tận cùng của các số tự nhiên có tận cùng là 2; 4;8 khi nâng lên lũy thừa 4n (n # 0) đều có chữ số tận cùng là 6

* Cho Học Sinh tính:

2 ⁴ = …6 ; 2 ⁸ = …6 ; 2 ¹² = …6

4 ⁴ =…6 ; 4 ⁸ = …6 ; 4¹² = …6

8 ⁴ = …6; 8 ⁸ = …6; 8 ¹² = …6 

 Các số tự nhiên có chữ số tận cùng bằng 2;4;8 khi nâng lên lũy thừa 4n ( n # 0) đều có chữ số tận cùng là 6

* Tương tự cho Học Sinh tính : ( Vận dụng chữ số tận cùng của một tích)

3⁴ =…1 ; 3⁸ = …1; 3 ¹² = …1

7⁴ = …1; 7⁸ = …1 ; 7 ¹² = …1

9⁴ = …1 ; 9 ⁸ = …1 ; 9 ¹² = …1 

Các số tự nhiên có chữ số tận cùng là 3; 7; 9 nâng lên lũy thừa 4n (n # 0) có chữ số tận cùng là 1 

* Chú ý: 

1. 1. • 
        Riêng đối với các số tự nhiên có chữ số tận cùng là 4 hoặc 9 : 

+ Nếu nâng lên lũy thừa lẽ đều có chữ số tận cùng là chính nó

+ Nếu nâng lên lũy thừa chẵn thì có chữ số tận cùng là 6 và 1

1. 1. • 
        Một số chính phương thì không có chữ số tận cùng là 2; 3; 7; 8 
      •