Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1:
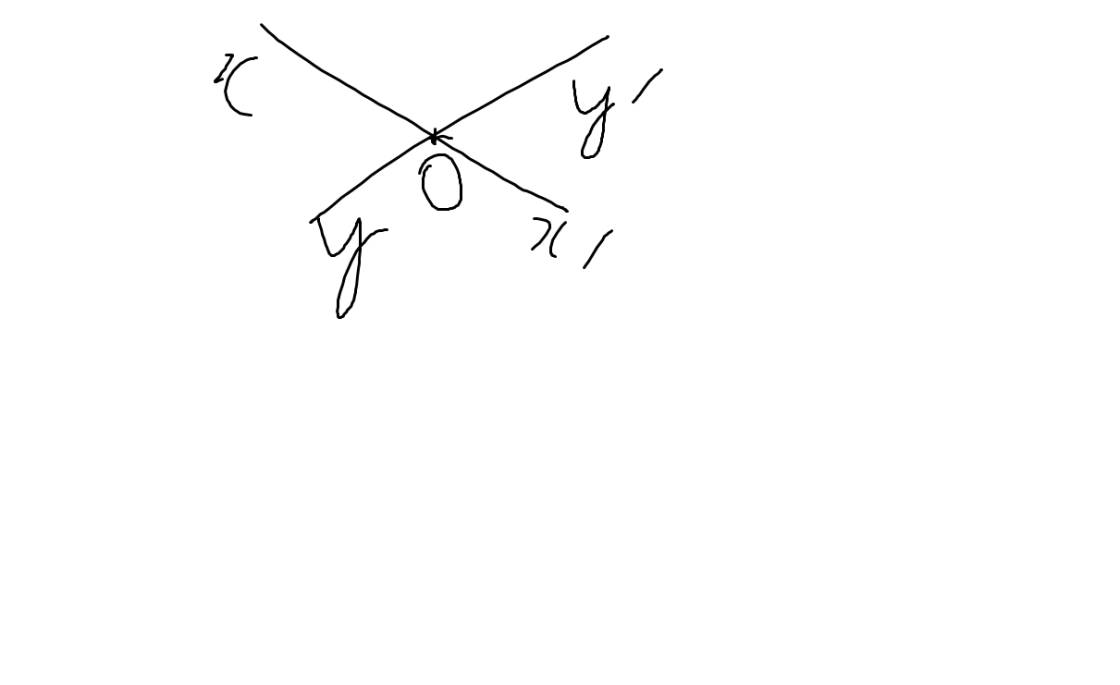
a: Hai cặp góc đối đỉnh là \(\widehat{xOy};\widehat{x'Oy'}\) và \(\widehat{xOy'};\widehat{x'Oy}\)
b: hai cặp góc bù nhau là:
\(\widehat{xOy};\widehat{xOy'}\)
\(\widehat{x'Oy};\widehat{x'Oy'}\)

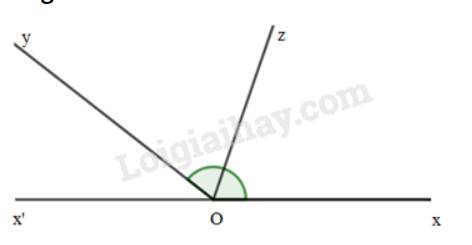
Vì Oz là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.142^\circ = 71^\circ \)
Mà \(\widehat {x'Oz}\) và \(\widehat {xOz}\) là 2 góc kề bù nên \(\widehat {xOz} + \widehat {x'Oz} = 180^\circ \Rightarrow 71^\circ + \widehat {x'Oz} = 180^\circ \Rightarrow \widehat {x'Oz} = 180^\circ - 71^\circ = 109^\circ \)
Vậy \(\widehat {x'Oz} = 109^\circ \)

a) góc xOy và góc yOz kề bù (GT)
=> góc xOy + góc yOz = 180 độ (t/c)
Mà góc xOy = 2 . góc yOz (GT)
=> 2 . góc yOz + góc yOz = 180 độ (t/c bắc cầu)
3 . góc yOz = 180 độ
góc yOz = 60 độ (1)
b) xOy và yOz là 2 góc kề bù (GT)
=> Ox và Oz đối nhau
xOy' và yOz là 2 góc đối đỉnh (do Oy và Oy' đối nhau; Ox và Oz đối nhau)
=> góc xOy' = góc yOz (2)
Từ (1) và (2) => góc xOy' = 60 độ (t/c bắc cầu)
c) Các cặp góc đối đỉnh: xOy' và yOz; xOy và y'Oz

Ta có xOy + yOz = 180o (kề bù)
Mà xOy = 2yOz <=> \(\frac{xOy}{2}=\frac{yOz}{1}=\frac{xOy+yOz}{2+1}=\frac{180^o}{3}=60^o\)
=> xOy = 60o . 2 = 120o
yOz = 60o . 1 = 60o

a) Các cặp góc kề bù
\(\widehat{xOy}\) và \(\widehat{yOx'}\)
\(\widehat{yOx'}\) và \(\widehat{x'Oy'}\)
\(\widehat{x'Oy'}\) và \(\widehat{xOy'}\)
\(\widehat{xOy'}\) và \(\widehat{xOy}\)
Các cặp góc đối:
\(\widehat{xOy}\) và \(\widehat{x'Oy'}\)
\(\widehat{x'Oy}\) và \(\widehat{y'Ox}\)
b) Do \(\widehat{xOy}\) kề bù với \(\widehat{xOy'}\)
\(\Rightarrow\widehat{xOy}+\widehat{xOy'}=180^o\)
\(\Rightarrow\widehat{xOy'}=180^o-70^o=110^o\)
1:
a: Các cặp góc đối đỉnh là: \(\widehat{aOb}';\widehat{a'Ob}\); \(\widehat{aOb};\widehat{a'Ob'}\)
b: Các cặp góc kề bù là: \(\widehat{aOb};\widehat{aOb'}\); \(\widehat{aOb'};\widehat{b'Oa'}\); \(\widehat{b'Oa'};\widehat{bOa'}\); \(\widehat{aOb};\widehat{a'Ob}\)
2:
Oz là phân giác của góc xOy
=>\(\widehat{xOz}=\dfrac{\widehat{xOy}}{2}=\dfrac{142^0}{2}=71^0\)
Ta có: \(\widehat{xOz}+\widehat{x'Oz}=180^0\)(hai góc kề bù)
=>\(\widehat{x'Oz}=180^0-71^0=109^0\)