
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


e,\(3\frac{2}{7}x-\frac{1}{8}=2\frac{3}{4}\)
\(=>\frac{23}{7}x-\frac{1}{8}=\frac{11}{4}\)
\(=>\frac{23}{7}x=\frac{11}{4}+\frac{1}{8}=\frac{23}{8}\)
\(=>x=\frac{23}{8}:\frac{23}{7}\)
\(=>x=\frac{7}{8}\)

b) \(5\frac{1}{4}.\frac{3}{8}+10\frac{3}{4}.\frac{3}{8}\)
\(=\left(5\frac{1}{4}+10\frac{3}{4}\right).\frac{3}{8}\)
\(=16.\frac{3}{8}=6\)
c) \(6\frac{1}{5}.\frac{-2}{7}+14\frac{4}{5}.\frac{-2}{7}\)
\(=\left(6\frac{1}{5}+14\frac{4}{5}\right).\frac{-2}{7}\)
\(=21.\frac{-2}{7}=-6\)


1125 : 1123- 35:9 - 60
1125: 1123- 243 : 9 - 60 121 - 243 : 9 - 60 = 34

125.100 - 25(9.4 +64)= 12500 - 25 (36+64) = 12500- 25.100=12500-2500=10000

\(\Rightarrow\dfrac{5}{4}-\dfrac{1}{4}x=\dfrac{3}{10}x-\dfrac{2}{5}\)
\(\Rightarrow\dfrac{5}{4}+\dfrac{2}{5}=\dfrac{3}{10}x-\dfrac{1}{4}x\)
\(\Rightarrow\dfrac{33}{20}=\dfrac{11}{20}x\)
\(\Rightarrow x=\dfrac{33}{20}\div\dfrac{11}{20}\)
\(\Rightarrow x=3\)
\(1\dfrac{1}{4}-x\dfrac{1}{4}=x\cdot30\%\cdot\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{5}{4}-x\dfrac{1}{4}=x\cdot\dfrac{3}{10}-\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{5}{4}-\dfrac{1}{4}x=\dfrac{3}{10}x-\dfrac{2}{5}\)
\(\Leftrightarrow25-5x=6x-8\)
\(\Leftrightarrow-5x-6x=-8-25\)
\(\Leftrightarrow-11x=-33\)
\(\Leftrightarrow x=3\)
Vậy x = 3
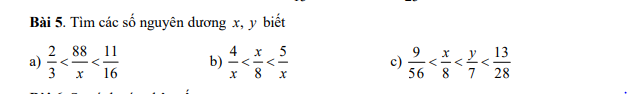

 Giúp vs ạ, gấp ạ, cảm ơn trc! Trình bày đầy đủ
Giúp vs ạ, gấp ạ, cảm ơn trc! Trình bày đầy đủ Giúp vs ạ, cần gấp, cảm ơn trc! Trình bày đầy đủ
Giúp vs ạ, cần gấp, cảm ơn trc! Trình bày đầy đủ








a: =>88/132<88/x<88/128
=>132>x>128
hay \(x\in\left\{131;130;129\right\}\)
c: =>9/56<7x/56<8y/56<26/56
=>\(\left\{{}\begin{matrix}7x\in\left\{14;21\right\}\\8y\in\left\{16;24\right\}\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(2;2\right);\left(3;3\right)\right\}\)