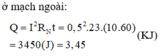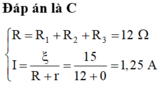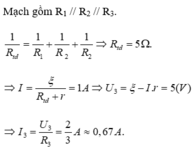Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

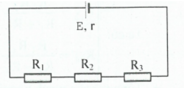
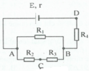
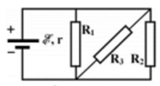
a) Mạch ngoài: \(\left(R_2//R_3\right)ntR_1\)
Điện trở mạch AB là:
\(R_{AB}=R_1+\dfrac{R_2R_3}{R_2+R_3}=3+\dfrac{4\cdot6}{4+6}=5,4\Omega\)
b) Cường độ dòng điện ở mạch chính:
\(I=\dfrac{E}{R_{AB}+r}=\dfrac{12}{5,4+0,6}=2A\)
Hiệu điện thế qua điện trở \(R_1\):
\(U_1=I_1R_1=2\cdot3=6V\)
Hiệu điện thế ở \(R_2,R_3\):
\(U_{23}=U-U_1=I\cdot R_{AB}-U_1=2\cdot5,4-6=4,8V\)
Cường độ dòng điện đi qua \(R_2,R_3\):
\(I_2=I_3=\dfrac{U_{23}}{R_{23}}=\dfrac{4,8}{\dfrac{R_2R_3}{R_2+R_3}}=\dfrac{4,8}{\dfrac{4\cdot6}{4+6}}=2A\)

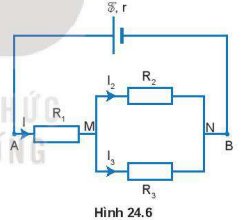
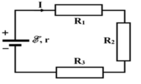
Ta có: R 23 = R 2 + R 3 = 6 Ω ⇒ R A B = R 1 . R 23 R 1 + R 23 = 2 Ω
Tổng trở của mạch ngoài: R n g = R A B + R 4 = 8 Ω
Cường độ dòng điện trong mạch chính: I = E R n g + r = 1 ( A ) ⇒ I 4 = 1 ( A )
Chọn A

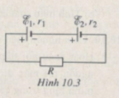
Theo sơ đồ Hình 10.3 thì hai nguồn đã cho được mắc nối tiếp với nhau, áp dụng định luật Ôm cho toàn mạch ta tính được cường độ dòng điện chạy trong mạch là: I 1 = 0,9 A

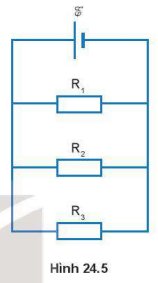
Ta có: R1 ∥ R2 ∥ R3
Điện trở tương đương của mạch là: \(\frac{1}{{{R_{td}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + \frac{1}{{{R_3}}} \Rightarrow {R_{td}} = \frac{{200}}{{19}}\Omega \)
a) Cường độ dòng điện chạy qua điện trở R1: I1 = \(\frac{\xi }{{{R_1}}} = \frac{{10}}{{20}}\)= 0,5(A)
b) Cường độ dòng điện chạy qua mạch điện chính: I = \(\frac{\xi }{{{R_{td}}}} = \frac{{10}}{{\frac{{200}}{{19}}}}\)= 0,95(A).