
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{\dfrac{5}{4}}=\dfrac{b}{\dfrac{6}{5}}=\dfrac{c}{\dfrac{11}{10}}=\dfrac{a+b+c}{\dfrac{5}{4}+\dfrac{6}{5}+\dfrac{11}{10}}=\dfrac{710}{\dfrac{71}{20}}=200\)
Do đó: a=250; c=240; c=220

Bài 2:
a: Xét ΔAMN và ΔAMP có
AM chung
MN=MP
AN=AP
Do đó: ΔAMN=ΔAMP

Bài 6:
a) Xét ΔBAC vuông tại A và ΔBAD vuông tại A có
BA chung
AC=AD(gt)
Do đó: ΔBAC=ΔBAD(hai cạnh góc vuông)
Suy ra: \(\widehat{CBA}=\widehat{DBA}\)(hai góc tương ứng)
hay BA là tia phân giác của \(\widehat{DBC}\)

Bạn tham khảo lời giải ở đây nhé: https://loigiaihay.com/bai-11-trang-169-tai-lieu-day-hoc-toan-7-tap-1-c243a39719.html


b: \(\sqrt{8^2+6^2}-\sqrt{16}+\dfrac{1}{2}\sqrt{\dfrac{4}{25}}\)
\(=10-4+\dfrac{1}{2}\cdot\dfrac{2}{5}=6+\dfrac{1}{5}=\dfrac{31}{5}\)

\(\text{#TNam}\)
`5,A`
Gọi các cạnh của Tam giác `ABC` lần lượt là `x,y,z (x,y,z \ne 0)`
`3` góc của tam giác lần lượt tỉ lệ với `2:3:4`
Nghĩa là: `x/2=y/3=z/4`
Tổng số đo `3` góc trong `1` tam giác là `180^0`
`-> x+y+z=180`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/2=y/3=z/4=`\(\dfrac{x+y+z}{2+3+4}=\dfrac{180}{9}=20\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{2}=20\\\dfrac{y}{3}=20\\\dfrac{z}{4}=20\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=20\cdot2=40\\y=20\cdot3=60\\z=20\cdot4=80\end{matrix}\right.\)
Vậy, độ dài các cạnh của Tam giác `ABC` lần lượt là `40^0, 60^0, 80^0`.
`6,B`
Gọi số người thợ của `3` nhóm lần lượt là `x,y,z (x,y,z \ne 0)`
Vì năng suất làm việc của các người thợ như nhau `->` số thợ và số ngày là `2` đại lượng tỉ lệ nghịch
`-> 40x=60y=50z` hay \(\dfrac{x}{\dfrac{1}{40}}=\dfrac{y}{\dfrac{1}{60}}=\dfrac{z}{\dfrac{1}{50}}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{\dfrac{1}{40}}=\dfrac{y}{\dfrac{1}{60}}=\dfrac{z}{\dfrac{1}{50}}=\dfrac{x-z}{\dfrac{1}{40}-\dfrac{1}{50}}=\dfrac{3}{\dfrac{1}{200}}=600\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{\dfrac{1}{40}}=600\\\dfrac{y}{\dfrac{1}{60}}=600\\\dfrac{z}{\dfrac{1}{50}}=600\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=600\cdot\dfrac{1}{40}=15\\y=600\cdot\dfrac{1}{60}=10\\z=600\cdot\dfrac{1}{50}=12\end{matrix}\right.\)
Vậy, số thợ của nhóm `1,2,3` lần lượt là `15,10,12`.

a, Theo định lí Pytago tam giác ABH vuông tại H
\(AH=\sqrt{AB^2-BH}=\sqrt{81-9}=6\sqrt{2}\)
Theo định lí Pytago tam giác AHC vuông tại H
\(HC=x=\sqrt{AC^2-AH^2}=7\)
b, Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AC^2=HC.BC=1600\Rightarrow AC=x=40\)


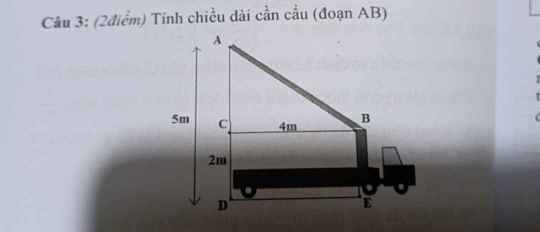
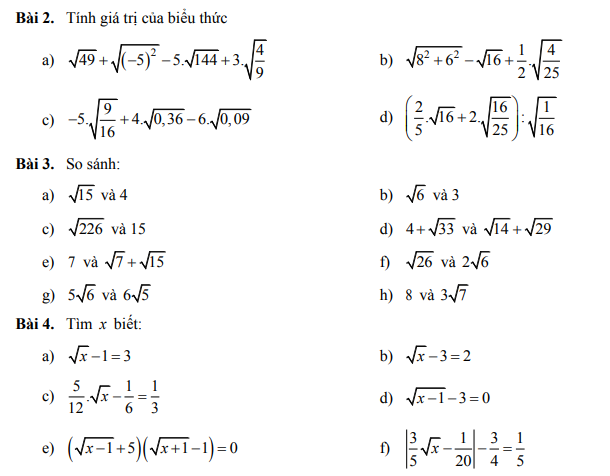 các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy
các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy
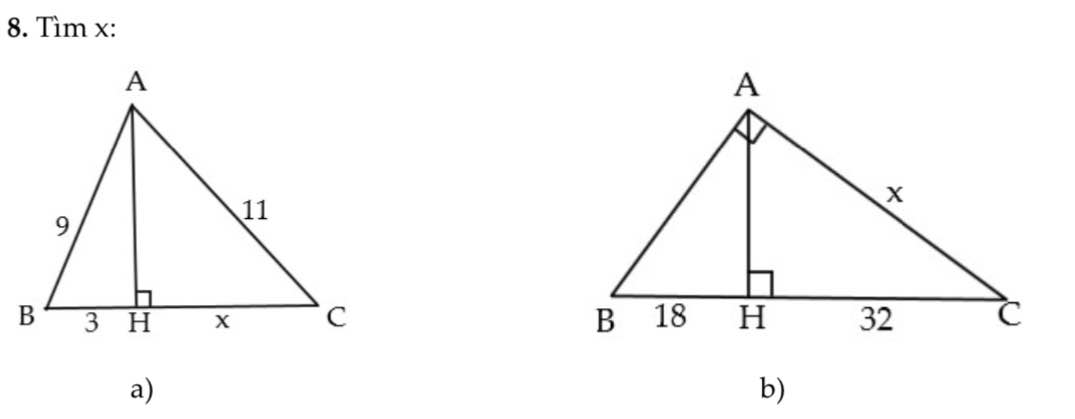
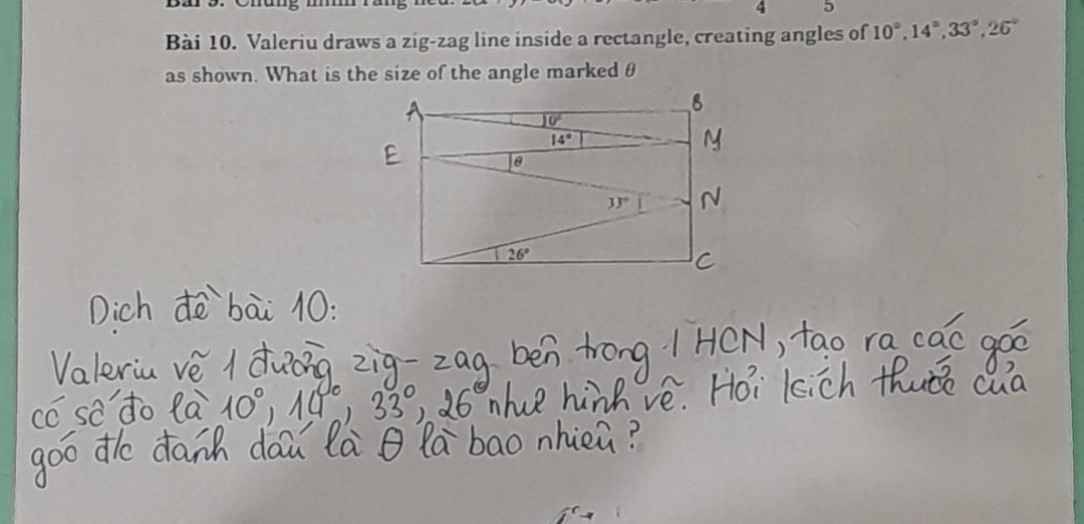
ta có : \(\frac{x}{7}=\frac{y}{4}=\frac{z}{2}\) = \(\frac{3z}{6}\)
theo tính chất của dãy tỉ số ta có :
\(\frac{x}{7}=\frac{y}{4}=\frac{3z}{6}\)= \(\frac{x-3z}{7-6}\)= \(\frac{9}{1}=9\)
\(\frac{x}{7}=9\Rightarrow x=9\times7=63\)
\(\frac{y}{4}=9\Rightarrow y=9\times4=36\)
\(\frac{z}{2}=9\Rightarrow z=9\times2=18\)