Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 4: Để tìm các chữ số a, b thỏa mãn các điều kiện, ta sẽ kiểm tra từng trường hợp.
a. Để số 4a12b chia hết cho 2, 5 và 9, ta cần xét chữ số cuối cùng b. Vì số chia hết cho 2, nên b phải là số chẵn. Vì số chia hết cho 5, nên b phải là 0 hoặc 5. Vì số chia hết cho 9, nên tổng các chữ số trong số đó phải chia hết cho 9. Ta thử từng trường hợp:
- Nếu b = 0, thì tổng các chữ số là 4 + a + 1 + 2 + 0 = 7 + a. Để 7 + a chia hết cho 9, ta có a = 2.
- Nếu b = 5, thì tổng các chữ số là 4 + a + 1 + 2 + 5 = 12 + a. Để 12 + a chia hết cho 9, ta có a = 6.
Vậy, các giá trị thỏa mãn là a = 2 hoặc a = 6, và b = 0 hoặc b = 5.
b. Để số 5a43b chia hết cho 2, 3 và 5, ta cần xét chữ số cuối cùng b. Vì số chia hết cho 2, nên b phải là số chẵn. Vì số chia hết cho 3, nên tổng các chữ số trong số đó phải chia hết cho 3. Vì số chia hết cho 5, nên b phải là 0 hoặc 5. Ta thử từng trường hợp:
- Nếu b = 0, thì tổng các chữ số là 5 + a + 4 + 3 + 0 = 12 + a. Để 12 + a chia hết cho 3, ta có a = 0 hoặc a = 3 hoặc a = 6 hoặc a = 9.
- Nếu b = 5, thì tổng các chữ số là 5 + a + 4 + 3 + 5 = 17 + a. Để 17 + a chia hết cho 3, ta có a = 1 hoặc a = 4 hoặc a = 7.
Vậy, các giá trị thỏa mãn là a = 0 hoặc a = 3 hoặc a = 6 hoặc a = 9, và b = 0 hoặc b = 5.
c. Để số 735a2b chia hết cho 5 và 9, nhưng không chia hết cho 2, ta cần xét chữ số cuối cùng b. Vì số chia hết cho 5, nên b phải là 0 hoặc 5. Vì số chia hết cho 9, nên tổng các chữ số trong số đó phải chia hết cho 9. Ta thử từng trường hợp:
- Nếu b = 0, thì tổng các chữ số là 7 + 3 + 5 + a + 2 + 0 = 17 + a. Để 17 + a chia hết cho 9, ta có a = 7 hoặc a = 8.
- Nếu b = 5, thì tổng các chữ số là 7 + 3 + 5 + a + 2 + 5 = 22 + a. Để 22 + a chia hết cho 9, ta có a = 2 hoặc a = 5 hoặc a = 8.
Vậy, các giá trị thỏa mãn là a = 2 hoặc a = 5 hoặc a = 7 hoặc a = 8, và b = 0 hoặc b = 5.
Bài 5: Để xác định xem tổng A có chia hết cho 8 hay không, ta cần tính tổng A và kiểm tra xem nó có chia hết cho 8 hay không.

a, Vì 12ab chia hết co cả 2 và 5 nên => b = 0
Thay vào, ta có 12a0 chia hết cho 3 khi và chỉ khi 1 + 2 + a + 0 chia hết cho 3 => 3 + a chia hết cho 3
=> a thuộc { 0; 3; 6; 9 }
b, Vì a47b chia hết cho 2, 5 nên => b = 0
Thay vào, ta thấy a470 chia hết cho 9 khi và chỉ khi a + 4 + 7 + 0 chia hết cho 9 => a + 11 chia hết cho 9
=> a = 7
c, Vì 7a3b chia hết cho 5 nên => b = 0 hoặc b = 5
Nếu b = 0 thì a thuộc { 2; 5; 8 }
Nếu b = 5 thì a thuộc { 0; 3; 6; 9 }
d, Vì 4a9b chia hết cho 5 nên b = 0, hoặc b = 5
Nếu b = 5 thì a thuôc { 0; 9 }
Nếu b = 0 thì a = 5
1) do 12ab chia hết cho cả 2 và 5 nên b=0
Mà 12ab chia hết cho 3 nên 1+2+a+b=3+a+0 chia hết cho 3
nên a=3; a=6; a=9.
2) Làm tương tự câu 1
3)do 7a3b chia hết cho 5 nên b=0 hoặc b=5
Nếu b=0=>a+7+3+0 chia hết cho 3(4a3b chia hết cho 3)
nên a=2; a=5; a=8
Nếu b=5=>a+7+3+5 chia hết cho 3
nên a=3; a=6; a=9
4) làm tương tự câu 3
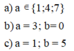
b ở đâu
b đâu ?