Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

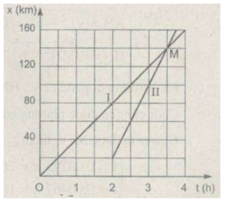
Trên đồ thị như ở hình vẽ
Vị trí và thời điểm ô tô đuổi kịp xe máy được biểu diễn bởi giao điểm M có tọa độ
x M = 140 km; t M = 3,5 h

a) Công thức tính quãng đường đi được của 2 xe là :
SA = VA.t = 60t và SB = VB.t = 40t.
Phương trình chuyển động của 2 xe:
xA = 0 + 60t và xB = 10 + 40t
Với S và x tính bằng km; t tính bằng giờ.
b)
| t(h) |
0 |
0,5 |
1 |
2 |
3 |
... |
| xA (km) |
0 |
30 |
60 |
120 |
180 |
... |
| xB (km) |
10 |
30 |
50 |
90 |
130 |
... |
c) Khi 2 xe gặp nhau thì tọa độ của chúng bằng nhau:
xA = xB
60t = 10 + 40t
⇒ 20t = 10
⇒ t = 0,5 h
⇒ xA = 60.0,5 = 30 km.
Vậy điểm gặp nhai cách gốc tọa độ A một đoạn 30 km.
Trên đồ thị điểm gặp nhai có tọa độ (t,x ) tương ứng là (0,5;30).

Đồ thị tọa độ của xe máy (đường I) và ô tô (đường II) được vẽ ở trên hình

a)
- Chọn gốc tọa độ O là vị trí ô tô bắt đầu đuổi theo xe khách và mốc thời gian là thời điểm ô tô đang ở O.
- Phương trình chuyển động của hai xe là:
+ Ô tô: \(x_1=v_1.t=60t\)
+ Xe khách: \(x_2=x_0+v_2.t=20+40t\)b) - Lập bảng biến thiên (tớ làm cái này chứ ít thấy người viết cái này bạn nhé)
| \(t\left(h\right)\) | \(0\) | \(1\) |
| \(x_1\left(km\right)\) | \(0\) | \(60\) |
| \(x_2\left(km\right)\) | \(20\) | \(60\) |
=> Ta vẽ được đồ thị của 2 xe như sau:

c) Dựa vào đồ thị cho ta biết thời điểm 2 xe gặp nhau là sau 1 giờ và tại vị trí có toạ độ \(60km\)
Bạn chưa tính x thì làm sao lập đồ thị được, bảng biến thiên có bị thiếu ko, thấy hơi kì





Bài 1:
a)
O A B x
Chọn gốc toạ độ tại A, chiều dương từ A đến B, mốc thời gian lúc 7h.
Ta có phương trình chuyển động thẳng đều là:
\(x=x_0+v.t\)
Với ô tô xuất phát từ A:
\(x_A=0+60t=60t\left(km\right)\)
Với ô tô xuất phát từ B:
\(x_B=180-40\left(t-0,5\right)=200-40t\left(km\right)\)
b)
Thời gian hai ô tô gặp nhau là:
\(x_A=x_B\Leftrightarrow60t=200-40t\)
\(\Rightarrow t=2\left(h\right)\)
Chỗ gặp nhau cách A quãng đường dài là:
\(60.2=120\left(km\right)\)
Chỗ gặp nhau cách B quãng đường dài là:
\(180-120=60\left(km\right)\)
c)
Thời gian ô tô xuất phát từ A đến B là:
\(t_1=\dfrac{S}{v_1}=\dfrac{180}{60}=3\left(h\right)\)
Thời gian ô tô xuất phát từ B đến A là:
\(t_2=\dfrac{S}{v_2}=\dfrac{180}{40}=4,5\left(h\right)\)