Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

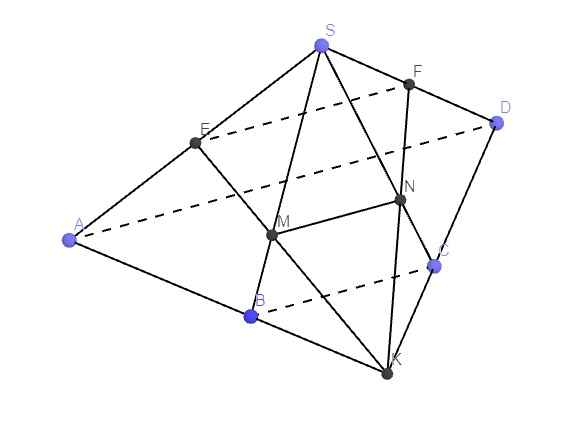
Áp dụng định lý Talet trong tam giác KAD:
\(\dfrac{KB}{KA}=\dfrac{KC}{KD}=\dfrac{BC}{AD}=\dfrac{1}{2}\)
\(\Rightarrow B,C\) lần lượt là trung điểm AK và DK
Mà E, F là trung điểm SA, SD
\(\Rightarrow\) M, N lần lượt là trọng tâm các tam giác SAK và SDK
\(\Rightarrow\dfrac{SM}{SB}=\dfrac{2}{3}\) ; \(\dfrac{SN}{SC}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{MN}{BC}=\dfrac{SM}{SB}=\dfrac{SN}{SC}=\dfrac{2}{3}\) (Talet)
\(\Rightarrow MN=\dfrac{2}{3}BC=\dfrac{2}{3}.\dfrac{1}{2}AD=\dfrac{1}{3}AD\)
Lại có EF là đường trung bình tam giác SAD \(\Rightarrow EF=\dfrac{1}{2}AD\)
\(\Rightarrow\dfrac{S_{KMN}}{S_{KEF}}=\dfrac{MN}{EF}=\dfrac{\dfrac{1}{3}AD}{\dfrac{1}{2}AD}=\dfrac{2}{3}\)

a.
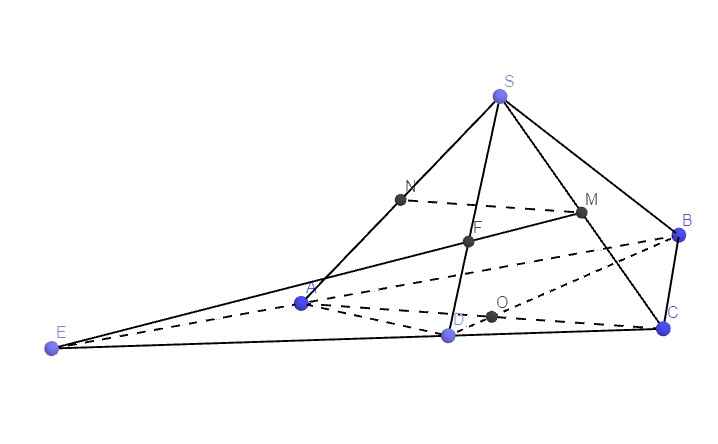
Do M là trung điểm SC, N là trung điểm SA \(\Rightarrow MN\) là đường trung bình tam giác SAC
\(\Rightarrow MN||AC\)
Mà \(AC\in\left(ABCD\right)\Rightarrow MN||\left(ABCD\right)\)
Gọi O là giao điểm AC và BD \(\Rightarrow O=\left(SAC\right)\cap\left(SBD\right)\)
\(S=\left(SAC\right)\cap\left(SBD\right)\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)
b.
Trong mp (ABCD), kéo dài AB và CD cắt nhau tại E
Trong mp (SCD), nối EM cắt SD tại F
\(\Rightarrow F=SD\cap\left(MAB\right)\)

Trong mp (ABCD), nối AN kéo dài cắt BC kéo dài tại E
⇒E∈(SBC)⇒E∈(SBC)
Do AD song song BE, áp dụng Talet:
ANNE=NDNC=1⇒AN=NE⇒ANNE=NDNC=1⇒AN=NE⇒ N là trung điểm AE
⇒MN⇒MN là đường trung bình tam giác SAE
⇒MN//SE⇒MN//(SBC)

Gọi E là giao điểm AB và CD
\(\Rightarrow E=\left(SAB\right)\cap\left(SCD\right)\)
\(\Rightarrow SE=\left(SAB\right)\cap\left(SCD\right)\)
b.
Do M là trung điểm SC, N là trung điểm BC
\(\Rightarrow MN\) là đường trung bình tam giác SBC
\(\Rightarrow MN||SB\)
Mà \(SB\in\left(SBD\right)\Rightarrow MN||\left(SBD\right)\)
c.
Trong mp (ABCD), nối AN cắt CD kéo dài tại F
Trong mp (SCD), nối FM kéo dài cắt SD tại G
\(\Rightarrow G=SD\cap\left(AMN\right)\)

a: \(E\in AC\subset\left(SAC\right)\)
\(E\in BD\subset\left(SBD\right)\)
Do đó: \(E\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SE\)
b: Gọi K là giao của AD với BC
\(K\in AD\subset\left(SAD\right)\)
\(K\in BC\subset\left(SBC\right)\)
Do đó: \(K\in\left(SAD\right)\cap\left(SBC\right)\)
mà \(S\in\left(SAD\right)\cap\left(SBC\right)\)
nên \(SK=\left(SAD\right)\cap\left(SBC\right)\)
c: AB//CD
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
Do đó: \(\left(SAB\right)\cap\left(SCD\right)=xy\), xy đi qua S và xy//AB//CD

a: \(E\in AC\subset\left(SAC\right);E\in BD\subset\left(SBD\right)\)
=>\(E\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SE\)
b: Gọi K là giao của AD và BC
\(K\in AD\subset\left(SAD\right);K\in BC\subset\left(SBC\right)\)
=>\(K\in\left(SAD\right)\cap\left(SBC\right)\)
mà \(S\in\left(SAD\right)\cap\left(SBC\right)\)
nên \(\left(SAD\right)\cap\left(SBC\right)=SK\)
c: Xét (SAB) và (SCD) có
AB//CD
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
Do đó: (SAB) giao (SCD)=xy; xy đi qua S và xy//AB//CD

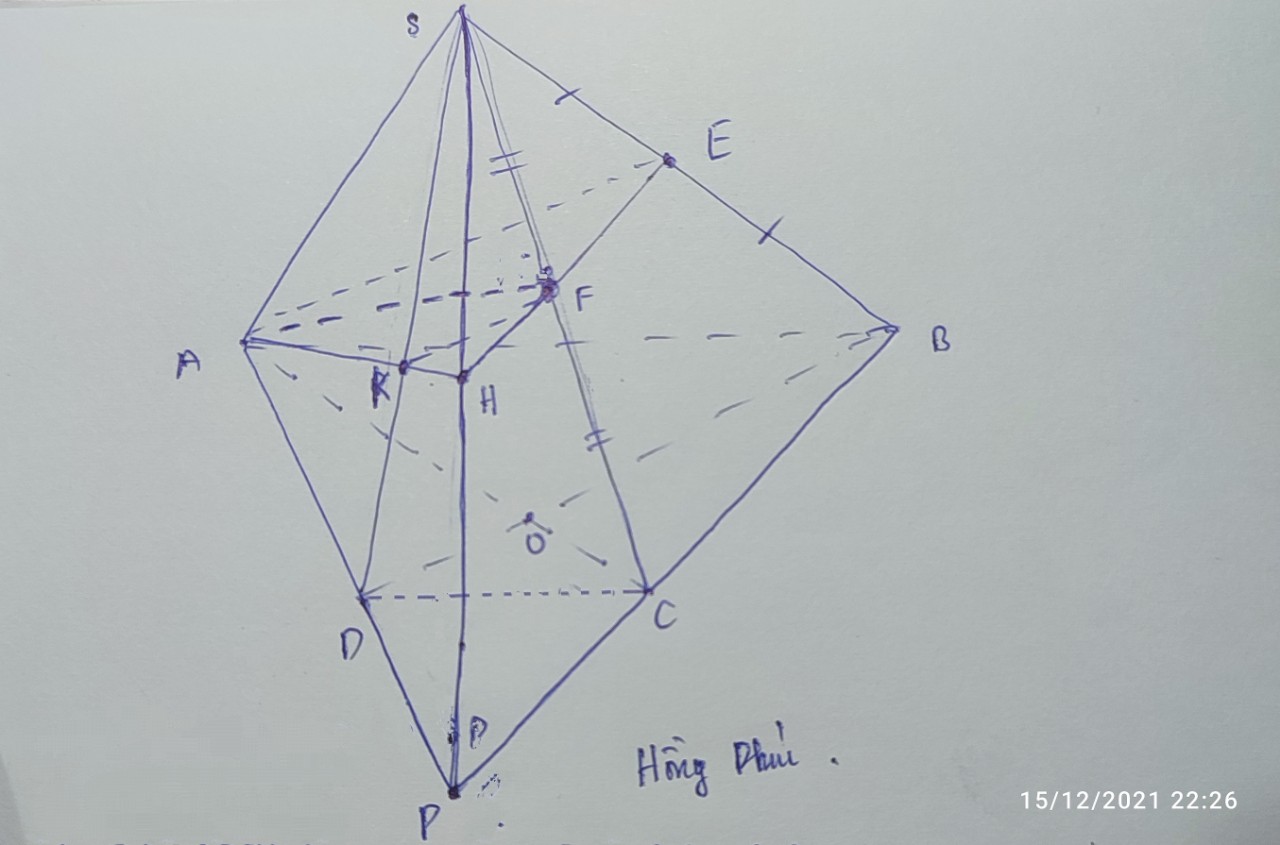
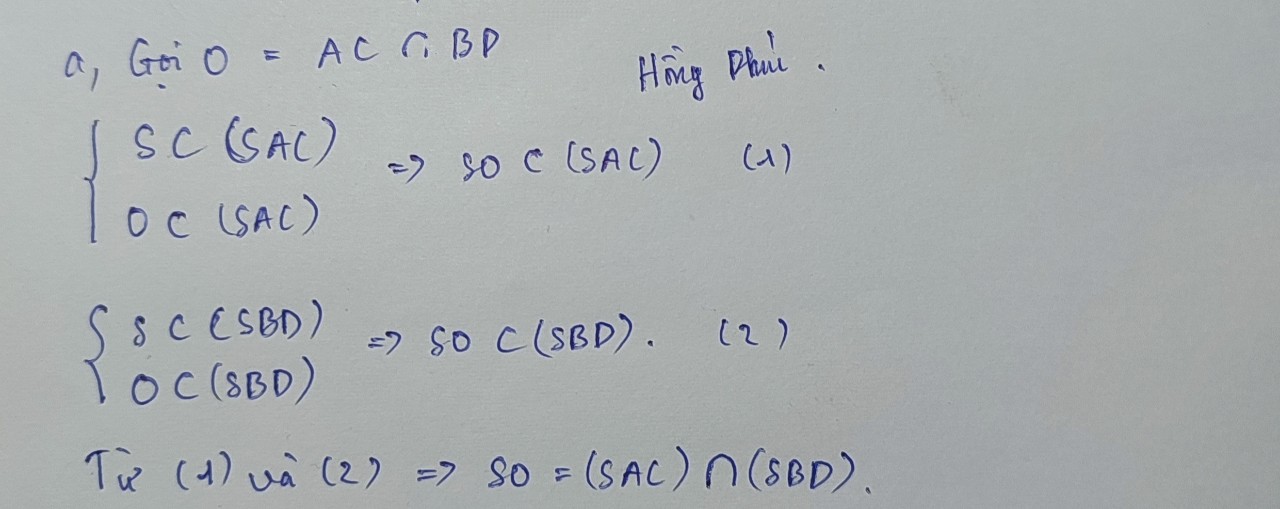
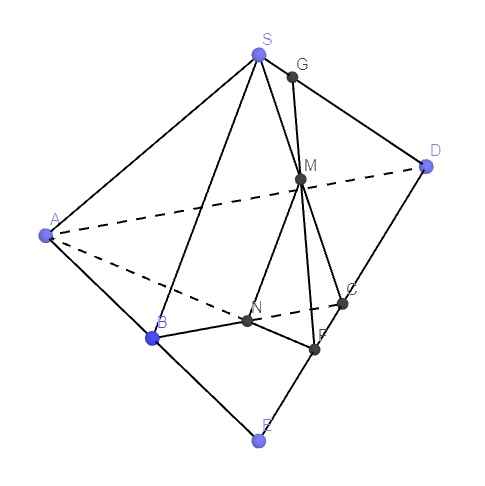
Gọi E là giao điểm của AC và BD \(\Rightarrow\left\{{}\begin{matrix}E\in\left(SAC\right)\\E\in\left(SBD\right)\end{matrix}\right.\)
\(\Rightarrow SE=\left(SAC\right)\cap\left(SBD\right)\)
Kéo dài AD và BC cắt nhau tại F
\(\Rightarrow SF=\left(SAD\right)\cap\left(SBC\right)\)
b.
Chắc là trung điểm của SC và SD?
M và trung điểm SC, N là trung điểm SD
\(\Rightarrow MN\) là đường trung bình tam giác SCD
\(\Rightarrow MN//CD\) , mà \(CD//AB\Rightarrow MN//AB\Rightarrow MN//\left(SAB\right)\)
Cảm ơn bạn