NN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BB
3
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 8 2021
11c.
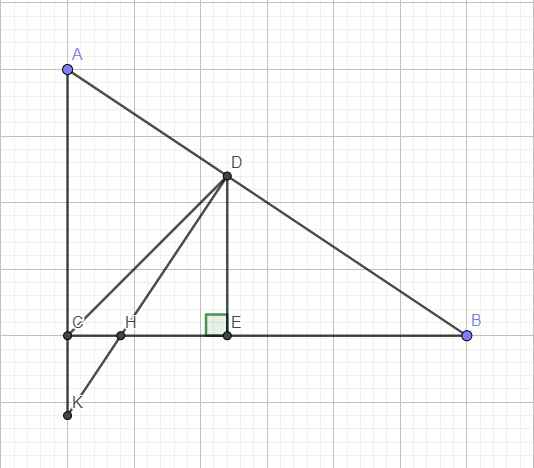
\(\left\{{}\begin{matrix}S_1^2=AD^2\\S_2^2=BD^2\end{matrix}\right.\) \(\Rightarrow\sqrt{S_1S_2}=AD.BD\) nên ta cần chứng minh: \(CD^2\le AD.BD\)
Kẻ \(DE\perp BC\Rightarrow\Delta CDE\) vuông cân tại E \(\Rightarrow CD^2=2DE^2\)
Mặt khác theo talet: \(\dfrac{DE}{AC}=\dfrac{BD}{AB}\Rightarrow DE=\dfrac{AC}{AB}.BD\Rightarrow2DE^2=2\dfrac{AC^2}{AB^2}.BD^2\)
Nên ta cần chứng minh: \(\dfrac{2AC^2}{AB^2}.BD^2\le AD.BD\Leftrightarrow\dfrac{2AC^2}{AB^2}\le\dfrac{AD}{BD}=\dfrac{AC}{BC}\)
\(\Leftrightarrow2AC.BC\le AB^2\)
Điều này đúng do: \(2AC.BC\le AC^2+BC^2=AB^2\) (đpcm)
Dấu "=" xảy ra khi D là trung điểm AB hay tam giác vuông cân tại C
N
0
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1 2022
22.
ĐKXĐ: \(y\ne1\)
\(\left\{{}\begin{matrix}x^2-\dfrac{1}{y-1}=2\\2x^2+\dfrac{3}{1-y}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x^2+\dfrac{2}{1-y}=4\\2x^2+\dfrac{3}{1-y}=2\end{matrix}\right.\)
Trừ pt dưới cho trên:
\(\Rightarrow\dfrac{1}{1-y}=-2\)
\(\Rightarrow1-y=-\dfrac{1}{2}\Rightarrow y=\dfrac{3}{2}\)
Thế vào \(x^2-\dfrac{1}{y-1}=2\)
\(\Rightarrow x^2=4\Rightarrow x=\pm2\)
Vậy nghiệm của hệ là \(\left(x;y\right)=\left(2;\dfrac{3}{2}\right);\left(-2;\dfrac{3}{2}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1 2022
b.
ĐKXĐ: \(x\ne-\dfrac{1}{2}\)
\(Hệ\Leftrightarrow\left\{{}\begin{matrix}2y^2-\dfrac{10}{2x+1}=8\\2y^2-\dfrac{11}{2x+1}=7\end{matrix}\right.\)
Trừ pt trên cho dưới:
\(\Rightarrow\dfrac{1}{2x+1}=1\)
\(\Rightarrow2x+1=1\)
\(\Rightarrow x=0\)
Thế vào \(y^2-\dfrac{5}{2x+1}=4\)
\(\Rightarrow y^2=9\Rightarrow y=\pm3\)
Vậy nghiệm của hệ là \(\left(x;y\right)=\left(0;3\right);\left(0;-3\right)\)
AH
Akai Haruma
Giáo viên
16 tháng 8 2021
Tại sao không giải ra $\sqrt{P}$ và $\sqrt{P}$?
Em đã có $P$ rồi, nhưng với $\sqrt{P}$, em làm sao rút gọn được khi mà $P$ đã khá gọn rồi. Cũng chẳng có giá trị nào của $x$ để tính cụ thể $P, \sqrt{P}$ rồi đi so sánh. Vì vậy cách này không khả thi.
Vậy thì phải tìm hướng khác. Muốn so sánh 2 số, ta xét hiệu hai số đó.
$P-\sqrt{P}=\sqrt{P}(\sqrt{P}-1)$
Rõ ràng $\sqrt{P}$ đã dương rồi, giờ ta phải xem xét xem $\sqrt{P}-1$ âm hay dương, hay $P$ có lớn hơn 1 không
Đó là lý do vì sao bài giải như trên.
AH
Akai Haruma
Giáo viên
16 tháng 8 2021
Còn câu hỏi khi nào giải ra từng cái $P$ và $\sqrt{P}$, thì đó là khi đề cho $x=2$ chả hạn, so sánh $P$ và $\sqrt{P}$.
Nhưg hầu như sẽ chẳng có đề nào ra kiểu vậy, mà đa số lợi dụng tính chất của phân thức đó để so sánh (ví dụ như trong bài tính chất nổi bật là $P>1$) cho nhanh. Đó là cái hay của đề bài.
TN
1
21 tháng 11 2021
giải bài 8 -> 11 giúp mình đang cần ;-;, mấy bài kia mình làm rồi nhưng chưa bt đúng sai
D
15 tháng 12 2022
B3
1) \(\sqrt{ }\)(2x-1)2 =5
\(\Leftrightarrow\) |2x-1| =5
\(\Leftrightarrow\) 2x-1 =5 hoặc 2x -1 = -5
\(\Leftrightarrow\) 2x=6 hoặc 2x= -4
\(\Leftrightarrow\) x=3 hoặc x= -2
2) 4-5x = 144
\(\Leftrightarrow\) -5x =140
\(\Leftrightarrow\) x= -60
3) \(\sqrt{ }\)(2x-2)2=2x-2
\(\Leftrightarrow\) | 2x -2 | =2x-2
\(\Leftrightarrow\) 2x-2 =2x-2 hoặc 2x-2 =-2x +2
\(\Leftrightarrow\) 0x=0 (loại ) hoặc x=2 ( nhận )
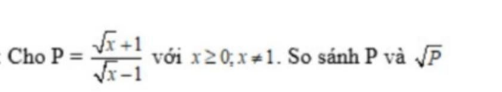
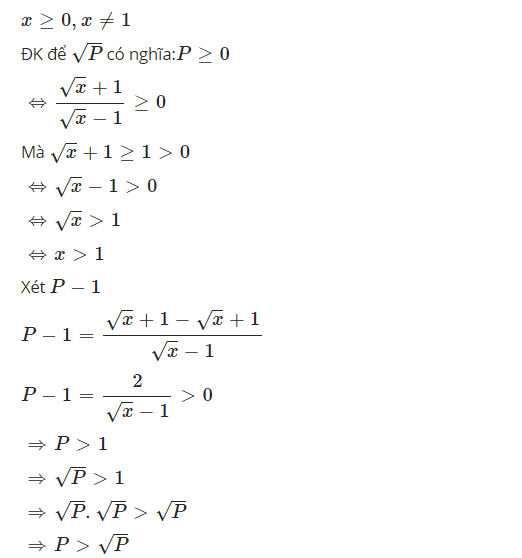
cái gì vậy bạn