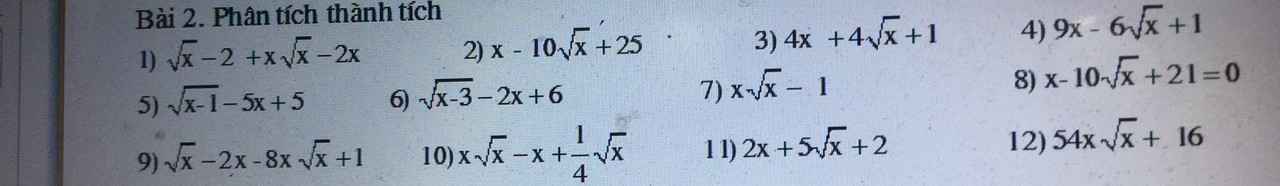K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
28 tháng 9 2016
\(\frac{693432080}{2008}\le a\le\frac{693432989}{2008}\)
345334 < a \(\le\)345335
=> a = 345335 => số cần tìm 693432680 vậy x = 6 và y = 0
3 tháng 10 2021
\(1,\\ a,=\dfrac{\sqrt{\left(\sqrt{a}-\sqrt{b}\right)^2}}{\sqrt{\left(\sqrt{a}-\sqrt{b}\right)}}=\sqrt{\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2}{\sqrt{a}-\sqrt{b}}}=\sqrt{\sqrt{a}-\sqrt{b}}\\ b,=\dfrac{\sqrt{\left(\sqrt{x}-\sqrt{3}\right)\left(\sqrt{x}+\sqrt{3}\right)}}{\sqrt{\sqrt{x}+\sqrt{3}}}\cdot\dfrac{\sqrt{3}}{\sqrt{\sqrt{x}-\sqrt{3}}}\\ =\sqrt{3}\\ c,=2y^2\cdot\dfrac{x^2}{\left|2y\right|}=\dfrac{2x^2y^2}{-2y}=-x^2y\\ d,=5xy\cdot\dfrac{\left|5x\right|}{y^2}=\dfrac{-25x^2y}{y^2}=\dfrac{-25x^2}{y}\)
3 tháng 10 2021
Bài 2:
a: Ta có: \(A=\left(3\sqrt{18}+2\sqrt{50}-4\sqrt{72}\right):8\sqrt{2}\)
\(=\left(9\sqrt{2}+10\sqrt{2}-24\sqrt{2}\right):8\sqrt{2}\)
\(=\dfrac{-5\sqrt{2}}{8\sqrt{2}}=-\dfrac{5}{8}\)
b: Ta có: \(B=\left(-4\sqrt{20}+5\sqrt{500}-3\sqrt{45}\right):\sqrt{5}\)
\(=\left(-8\sqrt{5}+50\sqrt{5}-9\sqrt{5}\right):\sqrt{5}\)
\(=49\)
LO
0
7 tháng 10 2021
a: \(x=\dfrac{6^2}{3}=12\left(cm\right)\)
\(y=\sqrt{6^2+12^2}=6\sqrt{5}\)
b: \(x=\sqrt{4\cdot9}=6\)
c: \(x=5\cdot\tan40^0\simeq4,2\left(cm\right)\)
AH
Akai Haruma
Giáo viên
23 tháng 7 2021
1.
\(\sqrt{x}-2+x\sqrt{x}-2x=(\sqrt{x}-2)+(x\sqrt{x}-2x)=(\sqrt{x}-2)+x(\sqrt{x}-2)\)
\(=(\sqrt{x}-2)(1+x)\)
2.
\(x-10\sqrt{x}+25=(\sqrt{x})^2-2.5.\sqrt{x}+5^2=(\sqrt{x}-5)^2\)
3.
\(4x+4\sqrt{x}+1=(2\sqrt{x})^2+2.2\sqrt{x}+1=(2\sqrt{x}+1)^2\)
4.
\(9x-6\sqrt{x}+1=(3\sqrt{x})^2-2.3\sqrt{x}+1=(3\sqrt{x}-1)^2\)
AH
Akai Haruma
Giáo viên
23 tháng 7 2021
5.
\(\sqrt{x-1}-5x+5=\sqrt{x-1}-5(x-1)=\sqrt{x-1}(1-5\sqrt{x-1})\)
6.
\(\sqrt{x-3}-2x+6=\sqrt{x-3}-2(x-3)=\sqrt{x-3}(1-2\sqrt{x-3})\)
7.
\(x\sqrt{x}-1=(\sqrt{x})^3-1^3=(\sqrt{x}-1)(x+\sqrt{x}+1)\)
8.
\(x-10\sqrt{x}+21=x-3\sqrt{x}-(7\sqrt{x}-21)\)
\(=\sqrt{x}(\sqrt{x}-3)-7(\sqrt{x}-3)=(\sqrt{x}-7)(\sqrt{x}-3)\)
FL
3
22 tháng 7 2017
\(B=\sin^247^o\times\cos45^o+\sin45^o\times\cos^247^o\)
\(B=\sin^247^o\times\cos45^o+\cos45^o\times\cos^247^o\)
\(B=\cos45^o\left(\sin^247^o+\cos^247^o\right)\)
\(B=\cos45^o.1=\cos45^o\)