Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đặt biểu thức ban đầu là A, 42020+42019+...+4+1=B
4B=42021 +42020 +42019+...+42+4
3B=4B-B=42021-1 => B= (42021-1)/3
A=75B+25=75(42021-1)/3 + 25= 25(42021-1)+25=25(42021-1+1)=25.42021=100.42020
=> A chia hết cho cả 100 và 42021
mặt khác A=25.42021=42021.(24+1)=24.42021+42021=6.42022+42021
vì 42021<42022 nên A chia 42022 dư 42021
tick cho mk nha!!!!!!!!

Câu 2:
\(C=3^{10}+3^{11}+3^{12}+...+3^{17}.\)
\(C=\left(3^{10}+3^{11}+3^{12}+3^{13}\right)+\left(3^{14}+3^{15}+3^{16}+3^{17}\right).\)
\(C=3^{10}\left(1+3+3^2+3^3\right)+3^{14}\left(1+3+3^2+3^3\right).\)
\(C=3^{10}\left(1+3+9+27\right)+3^{14}\left(1+3+9+27\right).\)
\(C=3^{10}.40+3^{14}.40.\)
\(C=\left(3^{10}+3^{14}\right).40⋮40\left(đpcm\right).\)
\(C=3^{10}+3^{11}+..+3^{17}\\ =\left(3^{10}+3^{11}+3^{12}+3^{13}\right)+\left(3^{14}+..+3^{17}\right)\\ =3^{10}\left(1+3+3^2+3^3\right)+3^{14}\left(1+3+3^2+3^3\right)\\ =40\left(3^{10}+3^{14}\right)⋮40\)

1) Ta có : 5xy + 2x - 5y = 7
=> x(5y - 2) - 5y + 2 = 7 + 2
=> x(5y - 2) - (5y - 2) = 9
=> (5y - 2)(x - 1) = 9
Với \(x;y\inℕ\Rightarrow\hept{\begin{cases}5y-2\inℕ^∗\\x-1\inℕ^∗\end{cases}}\)
=> có 9 = 3.3 = 1.9
Lập bảng xét các trường hợp
| x - 1 | 1 | 9 | 3 |
| 5y - 2 | 9 | 1 | 3 |
| x | 2 | 10 | 4(tm) |
| y | 2,2 | 0,6 | 1(tm) |
Vậy x = 4 ; y = 1
2) A = 75.(42018 + 42017 + .... + 42 + 4) + 25
Đặt B = 42018 + 42017 + .... + 42 + 4
Khi đó A = 75B + 25
<=> 4B = 42019 + 42018 + .... + 43 + 42
Lấy 4B trừ B cả 2 vế ta có :
4B - B = ( 42019 + 42018 + .... + 43 + 42) - (42018 + 42017 + .... + 42 + 4)
3B = 42019 - 4
=> B = \(\frac{4^{2019}-4}{3}\)
=> A = \(75\frac{4^{2019}-4}{3}+25=25.\left(4^{2019}-4\right)+25=25\left(4^{2019}-3\right)=25.4^{2019}-75\)
Vì \(25.4^{2019}⋮4^{2019}\Rightarrow25.4^{2019}-75:4^{2019}\text{ dư 75 }\Rightarrow A:4^{2019}\text{ dư 75}\)
Vậy số dư khi A chia cho 42019 là 75
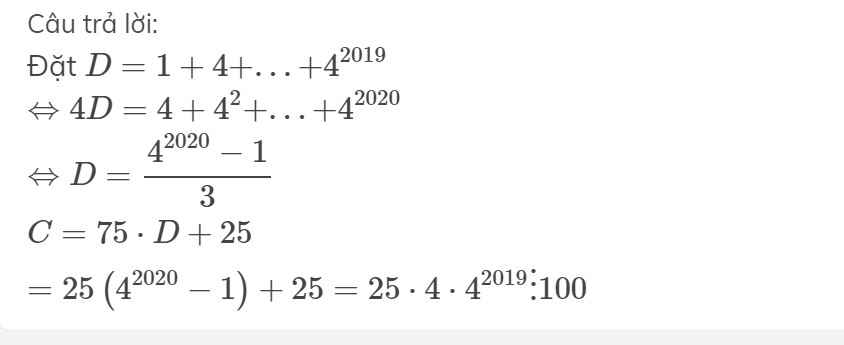
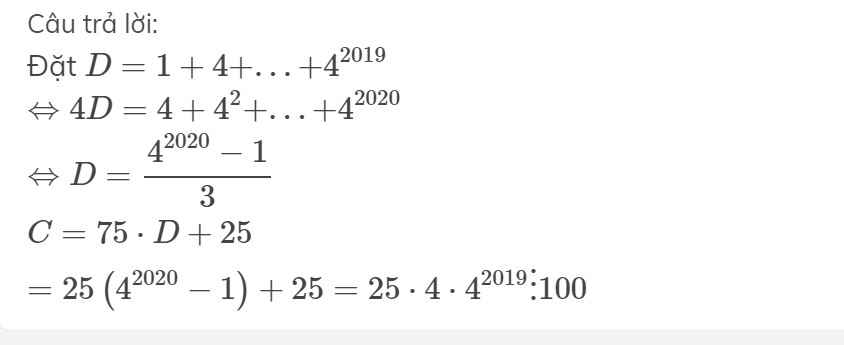
Đặt \(D=1+4+...+4^{2019}\)
\(\Leftrightarrow4D=4+4^2+...+4^{2020}\)
\(\Leftrightarrow D=\dfrac{4^{2020}-1}{3}\)
\(C=75\cdot D+25\)
\(=25\left(4^{2020}-1\right)+25=25\cdot4\cdot4^{2019}⋮100\)