Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bước sóng dài nhất trong dãy Ban me khi nguyên tử chuyển từ mức 3 về 2 --> \(\dfrac{hc}{\lambda_{32}}=E_3-E_2=-\dfrac{13,6eV}{3^2}+\dfrac{13,6eV}{2^2}\) --> \(\lambda _{32}\)
Bước sóng ngắn nhất trong dãy pasen khi nguyên tử chuyển từ mức vô cùng về 3 --> \(\dfrac{hc}{\lambda}=E_n-E_3=0+\dfrac{13,6eV}{3^2}\)--> \(\lambda\)

Theo giả thiết:
\(\lambda_1=\lambda_{21}=0,1216\mu m\)
\(\lambda_2=\lambda_{31}=0,1026\mu m\)
Bước sóng dài nhất trong dãy banme ứng với nguyên tử chuyển từ 3 về 2
Ta có: \(\dfrac{1}{\lambda_{31}}=\dfrac{1}{\lambda_{32}}+\dfrac{1}{\lambda_{21}}\)
\(\Rightarrow \dfrac{1}{0,1026}=\dfrac{1}{\lambda_{32}}+\dfrac{1}{0,1216}\)
\(\Rightarrow \lambda_{32}\)

Đáp án B
Bước sóng
λ
α
của vạch quang phổ
H
α
trong dãy Banme là 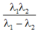

Bước sóng dài nhất trong dãy Banme là \(\lambda_1\Rightarrow\frac{hc}{\lambda_1}=E_3-E_2\)(1)
Bước sóng dài nhất trong dãy Laiman là \(\lambda_2\Rightarrow\frac{hc}{\lambda_2}=E_2-E_1\)(2)
Bước sóng dài thứ 2 trong dãy Laiman là \(\lambda_3\Rightarrow\frac{hc}{\lambda_3}=E_3-E_1\)(3)
Lấy (1) + (2) vế với vế ta đc: \(\frac{hc}{\lambda_1}+\frac{hc}{\lambda_2}=E_3-E_1=\frac{hc}{\lambda_3}\)
\(\Rightarrow\frac{1}{\lambda_3}=\frac{1}{\lambda_1}+\frac{1}{\lambda_2}\)
\(\Rightarrow\lambda_3=0,1029\mu m\)

Bước sóng dài nhất trong quang phổ Banmel sẽ là bước sóng ứng với bước chuyển từ 3 xuống 2
\(E=\frac{hc}{\lambda}=E_3-E_2=A\text{/}4-A\text{/}9\)
\(\Rightarrow A=2,18.10^{-19}J\)
Mình không hiểu câu hỏi của bạn lắm nhưng theo mình đoán bước sóng ngắn nhất này sẽ từ \(\text{n=∞ }\)
đến n=1
Năng lượng sẽ đúng bằng A
\(\lambda=\text{91,1528nm }\)

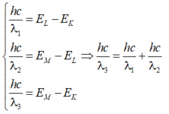
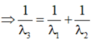
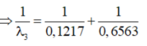
Hi, bạn chọn cho mình chuyên mục gì để dễ phân loại nhé.
Bước sóng dài nhất trong dãy Lai man khi nguyên tử chuyển từ mức 2 về 1 --> \(E_2-E_1=\dfrac{hc}{\lambda_{21}}\)
Bước sóng ngắn nhất trong dãy Ban me khi nguyên tử chuyển từ mức ngoài cũng về mức 2 --> \(E_{\infty}-E_2=\frac{hc}{\lambda_{\infty2}}\)
Năng lượng I ôn hóa nguyên tử Hiđro ứng với nguyên từ từ mức 1 chuyển lên mức vô cùng
\(\Rightarrow E=E_{\infty}-E_1=\frac{hc}{\lambda_{\infty1}}+\frac{hc}{\lambda_{21}}=\frac{hc}{\lambda}\)
\(\Rightarrow\frac{hc}{\lambda}=\frac{hc}{\lambda_{\infty1}}+\frac{hc}{\lambda_{21}}\)
\(\Rightarrow\frac{1}{\lambda}=\frac{1}{\lambda_{\infty1}}+\frac{1}{\lambda_{21}}\)
Bạn thay số vào tính nhé.